Dowód nierówności
Clown: Uzasadnij, że w dowolnym trójkącie (przy standardowych oznaczeniach) zachodzi nierówność:
a*cosα+b*cosβ+c*cosγ≤(a+b+c)/2
22 kwi 21:31
wredulus_pospolitus:
czym jest a,b,c ? czym jest α,β,γ ?
22 kwi 22:06
Clown:
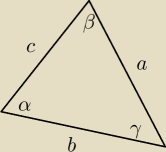
23 kwi 08:23
jc:
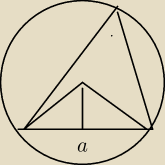
| | 1 | |
Pole trójkąta o wierzchołku w środku okręgu = |
| aR cos α |
| | 2 | |
Dlatego pole trójkąta wpisanego w okrąg
| | R | |
= P = |
| (a cos α + b cos β + c cos γ) |
| | 2 | |
Z drugiej strony
gdzie r jest promieniem okręgu wpisanego w trójkąt.
Wiemy, że r ≤ R/2. Stąd
| R | | a+b+c | | R | | a+b+c | |
| (a cos α + b cos β + c cos γ) = r* |
| ≤ |
| * |
| |
| 2 | | 2 | | 2 | | 2 | |
a więc
| | a+b+c | |
a cos α + b cos β + c cos γ ≤ |
| |
| | 2 | |
24 kwi 08:23

