Wykaż, że układ równań ma 3 rozwiązania Nova: Wykaż, że układ równań:

⎧	y=(x−2)2
⎩	(x−2)2=4−(y−2)2

Ma dokładnie trzy rozwiązania. Próbowałem podstawiać (x−2)²=t ale nie jestem w stanie dojść do tych trzech rozwiązań... Czy ktoś umiałby to rozpisać?

kerajs: wstawiasz (x−2)²=y do równania drugiego dostając równanie: y=4−(y−2)² Rozwiąż je

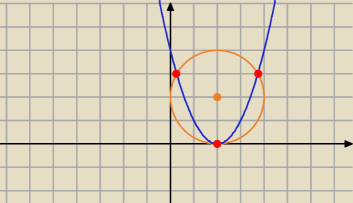
Eta: 1 sposób (algebraicznie) y=(x−2)² y=4−(y−2)² ⇒ y²−3y=0 ⇒ y(y−3)=0 ⇒ y=0 v y=3 dla y=0 (x−2)²=0 ⇒ x=2 , (2,0) dla y=3 (x−2)²=3 ⇒ x−2=√3 v x−2= −√3 ⇒ x=2+√3 v x= 2−√3 ( 2+√3,3) , (2−√3,3) 2 sposób (graficznie) y=(x−2)² −−− parabola o : (x−2)²+(y−2)²−4 −−− okrąg o środku S=(2,2) i promieniu r=2 i mamy trzy punkty wspólne więc układ ma trzy rozwiązania

Eta: Poprawiam zapis o : (x−2)²+(y−2)²=4

Nova: Bardzo dziękuję za pomoc!