dowód geometria równoległobok
anonim123: Udowodnij, że w równoległoboku ABCD zachodzi równość |AB|2+|BC|2+|CD|2+|DA|2=|AC|2+|BD|2
czy można to zrobić na wektorach bez układu współrzędnych?
21 kwi 16:54
anonim123: ?
21 kwi 17:16
chichi:
A może i można, a bo co? Spróbuj zobacz, a nie jak zwykle Pani GOTOWIEC
21 kwi 17:30
Eta:
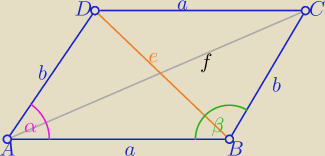
α+β=180
o to cosβ= −cosα
|AB|=|CD|=a i |BC|=|AD|=b
Dwa razy z tw. cosinusów
e
2=a
2+b
2−2abcosα
f
2=a
2+b
2+2ab cosα
+ −−−−−−−−−−−−−−−−−−−−−−−
e
2+f
2=a
2+a
2+b
2+b
2
i masz tezę

21 kwi 17:31
chichi:
Pani Gotowiec życzyła sobie na wektorach

P.S. Dowodziłbym tak samo jak
17:31 
21 kwi 17:33
anonim123: bo ja bym zrobiła coś takiego wektor AC=wektor AD+wektor AB i wektor BD=wektor BC+ wektor CD?
21 kwi 17:33
anonim123: czy tak można?
21 kwi 17:38
anonim123: ?
21 kwi 19:06
anonim123: ?
21 kwi 20:07
Mariusz:
anonim sugerowałbym napisać do Jakuba Grzegorzka
W równaniu okręgu wpisanego wygodniej było skorzystać z wektorów
ale czy tutaj coś da
21 kwi 20:38
anonim123: A może ktoś inny będzie wiedział?
21 kwi 20:45
Mila:
Napiszę trochę później.
21 kwi 21:55
Eta:
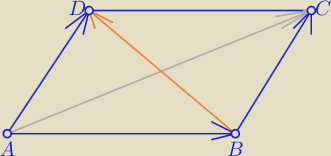
→ → → → →
AC=AB+BC |
2 ⇒ |AC|
2= |AB|
2+2AB o BC +|BC|
2
→ → → → →
BD= AD−AB |
2 ⇒ |BD|
2= |AD|
2−2AD o AB + |AB|
2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−
|AC|
2+|BD|
2= |AB|
2+|AD|
2+ |BC|
2 + |DC|
2 , bo |AB|
2=|DC|
2
===============================
21 kwi 22:09
Eta:
→ →
i AD= BC
21 kwi 22:12
Mila:

21 kwi 22:57
anonim123: Dziękuję

22 kwi 15:25
 α+β=180o to cosβ= −cosα
|AB|=|CD|=a i |BC|=|AD|=b
Dwa razy z tw. cosinusów
e2=a2+b2−2abcosα
f2=a2+b2+2ab cosα
+ −−−−−−−−−−−−−−−−−−−−−−−
e2+f2=a2+a2+b2+b2
i masz tezę
α+β=180o to cosβ= −cosα
|AB|=|CD|=a i |BC|=|AD|=b
Dwa razy z tw. cosinusów
e2=a2+b2−2abcosα
f2=a2+b2+2ab cosα
+ −−−−−−−−−−−−−−−−−−−−−−−
e2+f2=a2+a2+b2+b2
i masz tezę 
 P.S. Dowodziłbym tak samo jak 17:31
P.S. Dowodziłbym tak samo jak 17:31 
 → → → → →
AC=AB+BC |2 ⇒ |AC|2= |AB|2+2AB o BC +|BC|2
→ → → → →
BD= AD−AB |2 ⇒ |BD|2= |AD|2−2AD o AB + |AB|2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−
|AC|2+|BD|2= |AB|2+|AD|2+ |BC|2 + |DC|2 , bo |AB|2=|DC|2
===============================
→ → → → →
AC=AB+BC |2 ⇒ |AC|2= |AB|2+2AB o BC +|BC|2
→ → → → →
BD= AD−AB |2 ⇒ |BD|2= |AD|2−2AD o AB + |AB|2
+ −−−−−−−−−−−−−−−−−−−−−−−−−−−
|AC|2+|BD|2= |AB|2+|AD|2+ |BC|2 + |DC|2 , bo |AB|2=|DC|2
===============================

