Proszę o sprawdzenie janko: √x²+10x+25 ≥ 7− |x| czy dobra jest moja odpowiedź: x∊< −6,5>∪<1,∞)

PATMAT16: √x²+10x+25≥7−|x| √x²+10x+25=|x+5| |x+5|≥7−|x| x+5=0 ⇔ x=−5 x=0 Przedziały: (−∞;−5) <−5;0) <0:∞) x+5 − + + x − − + Opuszczamy w.bezwzględne |x+5|≥7−|x| dla x∊(−∞;−5) dla x∊<−5;0) dla x∊<0;∞) −(x+5)≥7−(−x) x+5≥7−(−x) x+5≥7−x −x−5≥7+x x+5≥7+x 2x≥2 /:2 −2x≥12 /:(−2) 5≥7 x≥1 x≤−6 x∊<1;∞) Zatem: x∊(−∞;−6> x∊(−∞;−6>∪<1;∞) Mi wyszło tak

chichi: Odp. z 13:41 jest poprawna

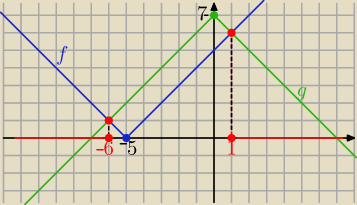Eta: graficznie f(x)=|x+5| i g(x)=−|x|+7 f(x) ≥g(x) odp: x∊(−∞, −6> U <1,∞)