Analityczna 0=0? PATMAT16: Dlaczego z pitagorasa na współrzędnych wychodzi mi 0=0? Punkt M(5;6) jest środkiem ramienia BC trójkąta równoramiennego ABC, w którym |AC|=|BC|.

	1
Podstawa AB tego trójkąta jest zawarta w prostej o równaniu: y=		x+1 oraz A(−3;0).Oblicz
	3

współrzędne punktu B. Zacząłem od tego, że wyznaczyłem równanie prostej prostopadłej do AB ,która przechodzi przez punkt M. W ten sposób znalazłem punkt leżący na prostej AB: D(6;3). Punkt B zapisałem tak:

	1
B(x;		x+1)
	3

Pitagoras: |MD|²+|DB|²=|MB|² Wyszło mi 0=0 Dlaczego taki szajs wychodzi? Zbyt ogólne opisanie współrzędnej punktu B? Rozumiem, że trzeba znaleźć inną prostą która nie tworzy trójkąta prostokątnego?

PATMAT16: To jest zadanie maturalne za 6 punktów z czerwca 2015 (rozszerzenie). Nie rozumiem sposobów przedstawionych przez nich...

PATMAT16: Wpadłem na jeszcze inny pomysł. Odległość punktu M od prostej AB jest wysokością trójkąta ABM. Odległość punktu B od prostej AM również jest wysokością tego trójkąta. Może wystarczy to wykorzystać? Tylko problem w tym czy niewiadomy punkt da się podstawić do prostej za x i y....

ite:

	3
Wskazówka: odległość |AD| =		|AB|
	4

rysunek z konstrukcją https://ibb.co/jJ0Msvg

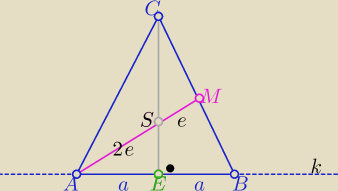
mat3: AM jest środkową to: → →

	1		7
AM =[8,6] więc SM=[5−x.6−y]=		[8,6] ⇒ S=(		,4)
	3		3

prosta CS ⊥ AB to

	7		1
CS: y= −3(x−		)+4 ⇒ CS : y= −3x+11 i AB : y= −		x+1
	3		3

rozwiązując układ równań danych tymi prostymi:

	⎧	y=−3x+11
	⎩	y=−13x+1

otrzymamy : E=(3,2) ====== zatem x_B=2x_E−x_A i y_B=2y_E−y_A x_B=9 i y_B=4 B=(9,4) =======

chichi: A no wychodzi 0=0, bo się zapętliłeś

chichi: @Eta fajnie wyszło, współrzędne pkt. B, są kwadratami współrzędnych pkt. E

Eta: