równanie okręgu anonim123: Napisz równanie okręgu przechodzącego przez punkt (1,−1) i przez punkty przecięcia okręgów x²+y²+2x−2y−23=0, x²+y²−6x+12y−35=0 próbowałam rozwiązać układ równań z równań okręgów nieszukanych ale nie wiem czy to coś da?

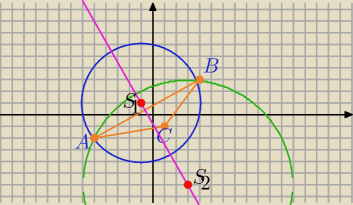
Mila: C=(1,−1) 1) x²+y²+2x−2y−23=0⇔ (x+1)²+(y−1)²−1−1−13=0 (x+1)²+(y−1)²=5² S₁=(−1,1) r=5 2) x²+y²−6x+12y−35=0 (x−3)²−9+(y+6)²−36−35=0 (x−3)²+(y+6)²=80 S₂=(3,−6), r=4√5 3) jedna symetralna (boku AB) przechodzi przez S₁ i S₂

	7		3
y=−		−
	4		4

Drugą napisz dla boku AC A=(−5,2) dokończ

Mila:

	7		3
y=−		x−
	4		4

Min. Edukacji: Okręgi nieszukane, co to takiego?

anonim: Skąd znamy współrzędne punktu A?

anonim123: Dziękuję😄

anonim:

Mila: Punkty A i B są punktami przecięcia okręgów. Musisz rozwiązać układ równań. x²+y²+2x−2y−23=0 x²+y²−6x+12y−35=0 Nie pisałam rozwiązania− zostawiłam to dla Ciebie.

Anonim: A no tak, a rozwiązać można np w taki sposób, odejmując stronami mamy 8x−14y+12= 0, x =... stąd A(−5,−2) więc masz błąd

Mila: Widać na rysunku, że A=(−5,−2), ostatnio robię literówki. Oglądam filmy i wpadam tylko na krótko na forum. Dzielnie sobie poradziłaś z układem Punkt B jaki masz? Wyjaśnię dlaczego nie wybrałam symetralnej AB. A może sama wiesz?