proszę o rozwiązanie anna: Podstawą graniastosłupa prostego ABCDEF GH jest romb o boku długości 5, polu 24 i kącie ostrym ∡BAD . Graniastosłup ten przecięto płaszczyzną AKLM w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym |∡KAM | = 45 . Oblicz pole tego przekroju.

janek191: Czy pole przekroju jest równe 18*(2 √2 + 1) ?

anna: nie znam wyniku zadanie (13) jest z próbnej matury 9 kwietnia 2022

an: P=18ctg22,5^o=18(√2+1)

anna: prosiłabym o rozwiązanie krok po kroku

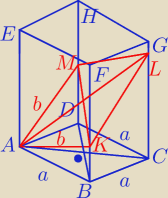
janek191: a = 5 Niech α = I ∡ BAD I Pole podstawy ( rombu): P_p = a²*sin α = 25*sin α = 24 więc

	24
sin α =
	25

zatem

	24		49
cos2α = 1 − (		)2 =
	25		225

	7
cos α =
	25

Niech d = I BD I Z tw. cosinusów

	7
d2 = a2 + a2 − 2 a*a*cos α = 2*25 − 50*		= 50 − 14 = 36
	25

d = 6 ==== I K M I = I BD I = d = 6 I AK I = I AM I = b więc d² = b² + b² −2 b²*cos 45^o

	√2
36 = 2 b2 − 2 b2*		= 2 b2 − √2 b2 =b2*( 2 − p{2])
	2

	36
b2 =		= 36 + 12 √2
	2 − √2

Pole przekroju

	√2
P = b2 *sin 45o = ( 36 + 12 √2)*		= 36 √2 + 18 = 18*(√2+ 1)
	2

====================================================

janek191: W ostatnim wierszu powinno być:

	√2
P = b2*sin 45o = (36 + 18 √2)*		= 18√2 + 18 = 18*(√2 + 1)
	2

anna: dziękuję bardzo