Dany jest trójkąt ABC o wierzchołkach A(-1;0) B(1;-2) C(1;4). Wyznacz równanie o Mat : Dany jest trójkąt ABC o wierzchołkach A(−1;0) B(1;−2) C(1;4). Wyznacz równanie okręgu opisanego na tym trójkącie. Chciałam obliczyć środek okręgu z tego ze symetralnej jest środkiem okręgu opisanego na trojkącie, ale mi nie wychodzi czy mógłby ktoś to policzyć proszę

Pr713: Prosta AB

⎧	0 = −a + b
⎩	−2 = a + b	⇒ aAB = −1

Symetralna AB, S₁(0, −1) oraz a_s1 = 1 y = x + b −1 = 0 + b b = −1 ⇒ y = x − 1 Prosta BC

⎧	−2 = a + b
⎩	4 = a + b	/ −

−6 = 2 − w ten sposób wyjdzie Ci sprzeczność, bo prosta ma równanie x = 1, ale wyznaczę je z postaci ogólnej żebyś zrozumiał Ax + By + C = 0

⎧	A − 2B + C = 0
⎩	A + 4B + C = 0	/ −

−6B = 0 ⇒ B = 0 A = −C + 2B = −C Zatem równanie prostej BC −Cx + C = 0 / : C −x + 1 = 0 x = 1 Symetralna BC, S₂ (1, 1) oraz a_s2 = 0 − prosta prostopadła do x = 1 w punkcie (1,1) ma równanie y = 1 Zatem środek to punkt przecięcia się symetralnych:

⎧	y = x − 1
⎩	y = 1

⎧	x = 2
⎩	y = 1

Promień to odległość środka okręgu O(2,1) od jednego z punktów A,B lub C lub którejś z prostych... Np. r = OA r² = (−1−2)²+(0−1)² = 10 Równanie okręgu (x−2)²+(y−1)² = 10

Pr713: Taki jeszcze komentarz do a_s2 Jeśli prosta ma równanie Ax + By + C₁ = 0 to prosta do niej prostopadła ma równanie −Bx + Ay + C₂ = 0 Zatem x − 1 = 0 −0x + 1y + C₁ = 0 y + C₁ = 0, S₂(1,1) 1 + C₁ = 0 C₁ = −1 Zatem y −1 = 0 ⇒ y = 1...

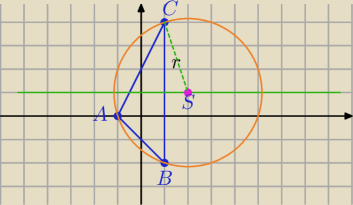
Mila: A(−1;0) B(1;−2) C(1;4). 1) s₁: y=1 jedna z symetralnych 2) Symetralna AC: (x+1)²+y²=(x−1)²+(y−4)²⇔ 2x=−2x−8y+16 s₂: 8y+4x−16=0 i punkt przecięcia z prostą y=1 4x=8 x=2 S=(2,1), r=|SC|=√5 ==============