Dwusieczna kąta w trapezie równoramiennym opisanym na okręgu Pomocy: Czy dwusieczna kąta w trapezie równoramiennym zawsze przecina środek okręgu wpisanego w ten trapez?

wredulus_pospolitus: nieee ... chociażby dlatego, że taki okrąg może w ogóle nie istnieć

Pomocy: okej, ale jeżeli mamy trapez równoramienny opisany na okręgu, wiemy że można go opisać, to czy wtedy zachodzi taka zależność?

wredulus_pospolitus: natomiast jeżeli już mamy załozone, że w trapez można wpisać okrąg to ... to wtedy TAK − odcinek łączący wierzchołek ze środkiem okręgu BĘDZIE dwusieczną tegoż kąta

Pomocy: dziękuję bardzo i miłego wieczoru życzę

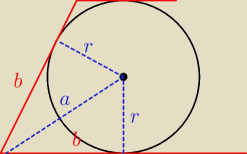
wredulus_pospolitus: co wynika z przystawania tychże trójkątów Co jest prawdą dla każdej pary trójkątów które powstają z każdego z czterech wierzchołków trapezu

wredulus_pospolitus: 'a' i 'r' są równe ... to są trójkąty prostokątne ... więc i 'b' jest równe związku z tym mamy trójkąty przystające (boki mają tą samą długość i znamy de facto wszystkie kąty −−− funkcje trygonometryczne)

Pomocy: jeszcze raz bardzo dziękuję, za wytłumaczenie i rysunek, często mi brakowało tej wiedzy przy rozwiązywaniu zadań z planimetrii, teraz powinno pójść dużo łatwiej

I'm back: Zauważ, że to będzie prawda dla dowolnego wielokąt w który można wpisać okrąg Dla każdego można będzie można podzielić na takie trójkąty prostokątne.