Równanie z parametrem Qwerty123: Wyznacz wszystkie wartości parametru a, dla których równanie 4x⁷−8x⁵ + a = 0 ma dokładnie trzy różne pierwiastki.

PATMAT16: Znajdź pochodną i wyznacz ekstrema f(x)=4x⁷−8x⁵+a f'(x)=28x⁶−40x⁴ /:4 f'(x)=7x⁶−10x⁴ f'(x)=x⁴(7x²−10) m₀ pochodnej: 1) 2) x⁴=0 7x²−10=0 7x²=10 /:7

	10
x2=		/ √
	7

	√70
x2=
	7

	√70
x3=−
	7

Pamiętaj, że pochodna w miejscu zerowym x⁴=0 odbije się od funkcji, ponieważ jest parzystego stopnia Znajdujesz ekstrema i argumenty oraz wartości dla których funkcja osiąga max i mim podstawiasz do funkcji f(x)=4x⁷−8x⁵+a. Za f(x) podstawiasz wartość, a za x argument. Tym sposobem znajdziesz "a" Powodzenia!

getin: f(x) = 4x⁷−8x⁵+a f'(x) = 28x⁶−40x⁴

	40		10
f'(x) = 28x4(x2−		)=28x4(x2−		)=28x4(x−√10/7)(x+√10/7)
	28		7

f'(x) = 0 gdy: x=0 (4−krotny) x=√10/7 (1−krotny) x=−√10/7 (1−krotny) f'(x)>0 gdy x ∊ (−∞; −√10/7) ∪ (√10/7;+∞) f'(x)<0 gdy x ∊ (−√10/7;0) ∪ (0; √10/7) f(x) rosnąca dla x ∊ (−∞; −√10/7), (√10/7;+∞) f(x) malejąca dla x ∊ (−√10/7;0), x ∊ (√10/7; +∞) teraz narysuję wykres pochodnej

PATMAT16: Ojj, tam powinno być: f'(x)=0 0=x⁴(7x²−10) Przepraszam, mój błąd

getin: Okej, podano wskazówki więc wstrzymam się od rysowania wykresów

Qwerty123: Okej, mam te 2 eksrema, gdzie mam później ich wstawić? Nie do końca rozumiem w którym miejscu

Qwerty123: "Znajdujesz ekstrema i argumenty oraz wartości dla których funkcja osiąga max i mim podstawiasz"

	√10		√10
Okej, mam ekstrema: Maksimum (−		) i minimum (		). Teraz jak mogę
	√7		√7

obliczyć te wartości? (Rozumiem, że argumenty, to są moje ekstrema, tak?)

PATMAT16:

	√10
Tam nie ma x=±		! Usuwamy niewymierność!
	√7

Otrzymujemy wtedy:

	√70
x=±
	7

Spójrz na moje rozwiązanie. Teraz przekształcasz równanie: 4x7−8x5 + a = 0 a=−4x⁷+8x⁵

	√70
Za x podstawiasz ±		i otrzymujesz "a" dla których wielomian ma trzy różne
	7

pierwiastki

Qwerty123: Aha, dziękuję! A obowiązkowo w tym przypadku mamy usuwać niewymierność?

PATMAT16: Wypada. Potem tylko ułatwia dalsze obliczenia

Qwerty123:

	√70
A czy to na pewno jest prawidłowe? Bo jak wstawiam np −		to otrzymuje zły wynik.
	7

	−1600√70
Prawidłowym wynikiem jest		= −5.57541041
	2401

	5200√70
U mnie zaś wychodzi wynik typu: −		= −18.1200839
	2401

Qwerty123: A nie, jednak jest dobrze, popełniałem błąd w obliczeniu. Dziękuję bardzo za pomoc!

PATMAT16: Git

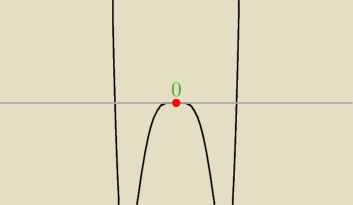
Qwerty123: A jak na przykład narysowałem wykres pochodnej funkcji i wygląda tak. Ona maleje od

	√70
−		i do 0, czy w punkcie 0 ta funkcja jest stała?
	7

ite: Dla x=0 wartość funkcji f(x)=4*x⁷−8*x⁵+a, gdzie a∊ℛ istnieje i jest określona jej wzorem f(0)=4*0⁷−8*0⁵+a=a. Dla pojedynczej wartości argumentu nie można określić, czy funkcja jest stała czy np.rosnąca, bo określenie monotoniczności polega na porównaniu wartości dla różnych argumentów.

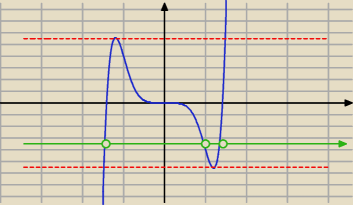
ite: Do lepszego zrozumienia zadania może się przydać wykres nie f.pochodnej ale funkcji f(x)=4*x⁷−8*x⁵ = 4x⁵(x−√2)(x−√2) Wtedy da się zobaczyć, w jakim zakresie można przesunąć wykres, żeby funkcja nadal miała trzy miejsca zerowe − a to przesunięcie (równoległe do osi OY) zależy właśnie od współczynnika a.

Anonim: a ∊ powinien wyjść przedział a nie pojedyńcze wartości

Pr713:

	1600√70		1600√70
a ∊ ( −		,		)
	2401		2401