Postać parametryczna prostej anonim123: W trójkącie ABC punkty E i D=(3,2) są środkami boków odpowiednio BC i AC wiemy również że wektor DE=[−3,1/2] i wektor AD=[4,2] a) wykaz że wektor DE=1/2 wektora AB b) wyznacz równania boków trójkąta (wskazówka wykorzystaj postać parametryczna prostej) Podpunkt a) rozwiązałam ale mam problem z b) https://zapodaj.net/f2d8babf9dea7.jpg.html https://zapodaj.net/538d995ee06cd.jpg.html

anonim123: skąd mam wiedzieć który punkt podstawić do równania postaci parametrycznej prostej?

anonim123: ?

anonim123: Chyba to jest nieistotne

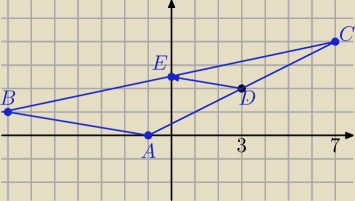
Mila: D=(3,2)− środek AC

	1
DE→=[−3,		],
	2

AD^→=[4,2] 1)

	1		1
D=(3,2)→T[−3,		]⇒E=(0,2		)
	2		2

D=(3,2)→T_{[−4, −2]}⇒A=(−1,0) D=(3,2)→T_4,2]⇒C=(7,4)

	3
2) CE→=[−7,−		]
	2

	1		3
E=(0,2		)→T[−7,−		]⇔B=(−7, 1)
	2		2

2) Równania : AC: A=(−1,0) , AD^→=[4,2] x=−1+4t y=2t, t∊R stąd możesz wyznaczyć postać np. ogólną 4t=x+1 2*(2t)=x+1 2y=x+1 ⇔x−2y+1=0 AC: BC: B=(−7,1) , BC^→=[14,3] x=−7+14t y=1+3t, t∊R stąd możesz wyznaczyć postać ogólną albo kierunkową

x+7
	=t
14

y−1
	=t
3

x+7		y−1
	=
14		3

dokończ sama

anonim123: Czyli jeżeli mam wyznaczyć AC to biorę punkt A nie C czy to obojętne?

anonim123: Jeżeli mam wyznaczyć równanie boku AC

Pr713: Dla punktu C możesz ten np. tak: DC^→ = [4,2], D(3,2) x = 3 + 4t

	y−2
y = 2 + 2t ⇒ t =
	2

x = 3 + 2y − 4 ⇒ x − 2y +1 = 0 Albo w ogóle jak masz współrzędne dwóch punktów to rozwiązujesz układ równań z postaci ogólnej prostych bądź kierunkowej i masz to samo....

Pr713: Ale tak jak Mila pisała, możesz też punkt C, wtedy C(7,4), AD^→ = [4,2] x = 7 + 4t = 7 + 2(2t) y = 4 + 2t x = 7 + 2(y−4) x = −1 + 2y x − 2y +1 = 0

anonim123: Czyli do równania boku AC mogę wziąć jakie punkty? A lub C?

anonim123: czyli np. C(7,4) i wektor AC=[4,2] i z tego wyznaczyć równanie parametryczne lub A=(−1,0) AC=[4,2]?

Pr713: Tak, możesz wektor AD, DC i AC oraz jeden z punktów A,D,C

anonim123: dzięki