Okrąg opisany na trapezie
Julka: Podstawy trapezu równoramiennego ABCD mają długości |AB| = 8 i |CD| = 6 oraz wysokośc równą 7.
Oblicz promień okręgu opisanego na tym trapezie.
α− kąt przy podstawie AB
Wyliczyłam ramię 5√2. Tym samym cos(α) = 1/5√2
|DB| = x
Z tw.Cosinusów
x2 = (5√2)2 + 64 − 2*8*5√2 * 1/5√2
x = √98
Po podstawieniu tego do twierdzenia sinusów wychodzą kosmiczne liczby, które nie są poprawnymi
odpowiedziami.
Z góry dziękuję za pomoc
15 kwi 16:12
Iryt:
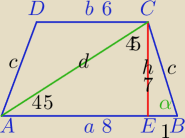
1)
|EB|=(8−6):2=1
|AE|=7
d=7
√2
2)
W ΔCED:
c
2=1+7
2=50
c=5
√2
3) Na trapezie równoramiennym można opisać okrąg
OKrąg opisany na ΔABC będzie jednocześnie opisany na podanym trapezie
| | 7 | | 5√2 | |
2R=7√2: |
| =7√2* |
| =10 |
| | 5√2 | | 7 | |
R=5
====
15 kwi 17:30
Mila:
II sposób
Bez tw. sinusów
1) W ΔABC:
|AB|=8, h=7 , c=5
√2, d=7
√2 ( obliczenia 17:30)
28*4R=56*10
4R=2*10
R=5
=====
15 kwi 17:43
 1)
|EB|=(8−6):2=1
|AE|=7
d=7√2
2)
W ΔCED:
c2=1+72=50
c=5√2
1)
|EB|=(8−6):2=1
|AE|=7
d=7√2
2)
W ΔCED:
c2=1+72=50
c=5√2