proszę o rozwiązanie anna: Dany jest trójkąt prostokątny ABC . Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta ABC , który ma mniejszą miarę. c − przeciwprostokątna p − połowa obwodu a , b przyprostokątne

	13
c = 6,5 r ⇒ c =		r
	2

	1		a+b+c		ab
P =		ab = pr =		r ⇒ r =
	2		2		a+b+c

	a
sinα =
	c

	b
cosα =
	c

dalej nie wiem jak

Eta:

	5
sinα=
	13

Eta:

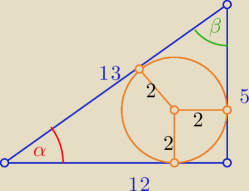
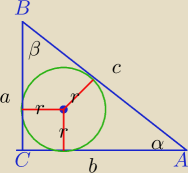Mila: c=6.5r a+b=2r+2R 1) a+b=2r+6.5r a+b=8.5r /:(c)

a		b		8.5
	+		=		⇔
c		c		6.5

	17
sinα+sinβ=
	13

2) (a+b)²=72.25 a²+2ab+b²=72.25 r² 2ab+c²=72.25r² 2ab=72.25r²−42.25r² 2ab=30r² ab=15r² / :c²

a		b		15r2
	*		=
c		c		42.25r2

	60
sinα* sinβ=
	169

3) Układ:

	17
sinα+sinβ=
	13

	60
sinα* sinβ=
	169

podstawienie:

	17
x+y=
	13

	60
x*y=
	169

	5		12
x=		, y=
	13		13

lub

	12		5
x=		, y=
	13		13

Posprawdzaj rachunki Jest kilka innych sposobów, może ktoś jeszcze napisze.

Pr713:

	a+b−c
Oczywiście Anna, równanie a+b = 2r + 2R, bierze się z zależności r =		, c = 2R
	2

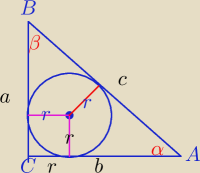Mila: 1)c=6.5r a+b=2r+6.5r⇔ a+b=8.5 stąd a=8.5r−b c²=a²+b² 2) (8.5r−b)²+b²=42.25r²⇔ 2b²−17br+30r²=0 r>0, b>0 Δ=49r²

	17r−7r		5
b=		=		r lub b=6r
	4		2

a=8.5r−2.5r=6r lub a=2,5r

	6r		12		2.5r		5
sinα=		=		lub sinα=		=
	6.5r		13		6.5r		13

odp .

	5
sinus mniejszego kąta:
	13

anna: dziękuję bardzo