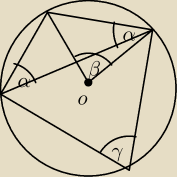
Miary stopniowe katów w okręgu Iorip: Witam, mam problem z zadaniem. Dane jakie dostałem to α = 38 stopni. Mam wyznaczyć miary stopniowe kątów β i γ. Wyszło mi że β = 52 stopni, a γ = 76 stopni, ale nie wiem czy zrobiłem to dobrze

Pr713: w trójkącie równoramiennym trzeci kąt = 180°−2*38° = 104°, z własności okręgu opisanego na czworokącie, suma miar kątów przeciwległych jest równa 180°, stąd kąt γ = 180°−104°=76°. Kąt β i α są to natomiast kąty: środkowy i wpisany oparte na tym samym łuku ⇒ β = 2α = 2*38° = 76°

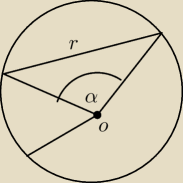
Iorip: Dzięki za odpowiedź, Wiesz może jak jeszcze to zrobić? Jedyne dane jakie miałem to to że jest to okrąg o(O,r) i że r wynosi r√3 Z góry dzięki.

Pr713: jeśli r = √3 tak jak napisałeś i jest to cięciwa z rysunku, to trójkąt jest równoboczny o boku √3. α = 60° Chyba, że zrobiłeś literówkę na rysunku i w poście, że R = r√3

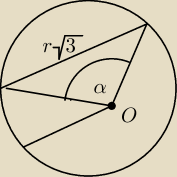
Iorip: Wybacz, rysunek był narysowany tak, poprawiłem. Chciałem tu skorzystać z tw. cosinusów ale wychodzi: cosα = r / −2

Pr713: i wtedy masz na myśli trójkąt o bokach: r, r i r√3 . Jeśli o to Ci chodziło, to skorzystaj z twierdzenia cosinusów. (r√3)² = r² + r² − 2*r*r*cosα 3r² = 2r² −2r²cosα 1 = −2cosα ⇒ cosα = −¹₂, cos(120°) = cos(180°− 60°) = −cos60° = −1/2, α = 120°

Iorip: ale w takim razie wychodzi tak jak napisałeś, 60*, dzięki

Iorip: 120*

Pr713: o to dobrze zgadłem treść zadania , rozwiązanie masz powyżej

Iorip: O, to dobrze myślałem

Iorip: Dziękuję

Pr713: