Sprawdź, jakim trójkątem jest trójkąt o bokach i pole koła opisanego na tym trój Pat: Sprawdź, jakim trójkątem jest trójkąt o bokach: a=6, b=3√2, c=3√10. Oblicz pole koła opisanego na tym trójkącie.

wredulus_pospolitus: 1) c > a > b 2) sprawdzamy jak się ma relacja c² do a² + b² to da nam odpowiedź na pytanie czy jest to trójkąt rozwartokątny, prostokątny, czy też ostrokątny 3) pole obliczamy z odpowiedniego wzoru (najpierw wyznaczamy 'r')

Pat: To czy jest rozwarty czy ostry to jako tako bym policzył(z cosinusów też można), ale problem jest z policzeniem pola trójkąta i policzeniem promienia. Jedyny wzór który znam na pole gdy są trzy boki, które są znane to z wzoru herona, a w przybliżeniu to wystarczy obliczyć sinus, ale czy jest inny sposób bez przybliżeń

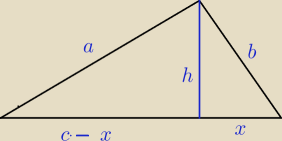
janek191: Mamy 36 = h² + ( 3√10 − x)² 18 = h² + x² −−−−−−−−−−−− odejmujemy stronami 18 = 90 − 6√10 x 6√10 x = 72 √10 x = 12

	12
x =		= 1,2 √10
	√10

h² = 18 − x² = 18 − 1,44*10 = 18 − 14,4 = 3,6 h = √3,6 Pole Δ = 0,5*3√10*√3,6 = 0,5*3*√36 = 9 ====================================

janek191:

	a*b*c
P =
	4 R

Mariusz: Janek a istnieje jakiś inny sposób wykazania poprawności tego wzorku niż z twierdzenia sinusów

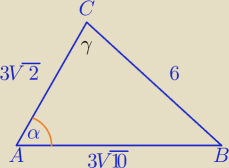
Mila: Jeżeli znasz tw. cosinusów, to można tak: 1) 6²=(3√10)²+(3√2)²−2*3√2*3√10 cosα 36−90−18=−18√20 cos α

	2
cosα=
	√5

	2
sin2α=1−(		)2
	√5

	1
sin2α=
	5

	1
sinα=
	√5

2) Z tw. sinusów

6
	=2R
1   √5

R=3√5 3) pole koła licz sam