wyliczenie współrzędnych punkty
Algorytm:
Jak mogę obliczyć współrzędne punktu C, wiedząc, że |AB| = 8, |AD| =
√712, |DC| =
√1852 i mając równanie prostej CD −> y=
56x +
54
Nie wiem kompletnie, jak można obliczyć współrzędne tego punktu.
11 kwi 22:53
wredulus_pospolitus:
To jest tyle co jest dane w zadaniu
Nie znasz współrzędnych żadnego z punktów A,B,C
11 kwi 23:11
Algorytm: A, znaczy znam, poza C
A(2,8) B(7,2) C ustaliłem, że jego punkty są (x, 56x+ 54) tylko nie mam pojęcia co
mogę zrobić dalej?
11 kwi 23:16
Algorytm: A sam trójkąt jest równoramienny
11 kwi 23:16
Algorytm: Trójkąt (ABC)
11 kwi 23:17
wredulus_pospolitus:
no to jak znasz punkty A i B to:
1) wyznaczasz wzór prostej przechodzącej przez punkty A i B (nie jest powiedziane, że AB ⊥ CD
)
2) wyznaczasz punkt D, jako punkt przecięcia się tych dwóch prostych
3) wyznaczasz punkt C leżący na danej prostej, odległy o daną wartość od punktu C
11 kwi 23:24
wredulus_pospolitus:
A skąd wiesz, że trójkąt ABC jest równoramienny
11 kwi 23:25
Algorytm: A nie mogłem stwierdzić, że AB ⊥ CD z powodu, że mamy trójkąt równoramienny i wtedy wysokość
prowadzona z wierzchołka C pada na podstawe AB pod kątem prostym?
11 kwi 23:25
Algorytm: A właśnie, |AB| jest podstawą tego trójkąta
11 kwi 23:26
Algorytm: Znaczy jest podane w książce
11 kwi 23:26
Algorytm: "Dany jest trójkąt równoramienny ABC o pdstawie AB i ramionach długości 8. Znając współrzędne
pkt A(2,8) oraz B(7,2) oblicz współrzędne pkt C, który leży na pierwszej połowie układu
współrzędnych"
11 kwi 23:27
wredulus_pospolitus:
Tu też masz trójkąt równoramienny ... tyle że CD nie jest wysokością tegoż trójkąta (gdzie jest
podane że jest jej wysokością i gdzie jest podane, że punkty ABC tworzą trójkąt równoramienny
)
11 kwi 23:27
Algorytm: Sorry, że nie podałem treści
11 kwi 23:27
wredulus_pospolitus:
To tak trudno podać PEŁNĄ treść zadania
No to |AB|
≠ 8
patrz treść zadania (AB to podstawa ... a ramiona mają długość 8
)
11 kwi 23:28
Algorytm: Ale punkt D u mnie to środek punktów AB
11 kwi 23:28
Algorytm: Aha, tak sorry, źle zobaczyłem
11 kwi 23:29
wredulus_pospolitus:
No to:
1) wzór okręgu o środku w punkcie A i promieniu r = 8
2) wzór okręgu o środku w punkcie B i promieniu r = 8
3) wyznaczasz punkty (dwa) przecięcia się tych okręgów
4) sprawdzasz który z tych punktów C1 czy też C2 leży w pierwszej połowie układu
współrzędnych (czyli x>0, y>0)
Koooniec
11 kwi 23:30
Algorytm: No dobra, ale jak mogę obliczyć współrzędne pkt C? Mam wzór prostej AB, czyli y = −65x +
525
11 kwi 23:30
Algorytm: Ahaaaaaaaaaaaaaaa, dzięki wielkie. To wtedy obliczenie prostej DC było nie potrzebne?
11 kwi 23:32
Algorytm: Bo właśnie w odpowiedziach jest dobrze jak u mnie, tylko że ostatni pkt z tym obliczeniem C nie
mam
11 kwi 23:32
wredulus_pospolitus:
jest zbyteczne
Oczywiście można, ale tam będzie trzeba więcej obliczeń wykonać i możesz się po drodze zaciukać
w pierwiastkach
11 kwi 23:34
Algorytm: a jaki był inny sposób jeszcze?
11 kwi 23:34
Algorytm: znaczy jest* xd, sorry, za dużo tej matmy xd
11 kwi 23:35
wredulus_pospolitus:
Inny
1) wyznaczasz współczynnik kierunkowy prostej AB (cała prosta jest zbyteczna) −−−> czyli:
| | 7+2 | | 2+8 | |
2) wyznaczasz środek odcinka AB −−−> ( |
| ; |
| ) = (4.5 ; 5) |
| | 2 | | 2 | |
3) wyznaczasz prostopadłą do AB przechodzącą przez punkt D(4.5 ; 5)
I teraz, np.:
4) wyznaczasz |AD|
5) wyznaczasz |CD| korzystając z tw. Pitagorasa
6) wracasz do równania prostej ... wyznaczasz punkt C odległy od D o wyznaczoną odległość
11 kwi 23:38
Algorytm: Właśnie ja te wszystkie punkty mam zrobione poza 6 od samego początku XD
11 kwi 23:40
Algorytm: A czy mógłbyś opisać bardziej w szczegółach 6 punkt?
11 kwi 23:41
Algorytm: bardziej szczegółowo*
11 kwi 23:42
wredulus_pospolitus:
możesz na przykład:
6.1) Napisać wzór okręgu o środku w D i promieniu równym |CD|.
6.2) Przecięcie się tego okręgu z prostą CD daje Ci punkty C1 i C2
11 kwi 23:43
Algorytm: Aha, dzięki wielkie, właśnie o to mi i chodziło xd
11 kwi 23:49
Algorytm: Czyli mogę obliczyć punkt Cy, że Dy + promień okręgu D?
11 kwi 23:52
Algorytm: A wtedy już znając Cy podstawiam do wzoru prostej DC? I wtedy Dy = 56Dx + 54?
11 kwi 23:54
wredulus_pospolitus:
C
y = D
y + r
a w życiu
11 kwi 23:55
Algorytm: Ah szkoda
11 kwi 23:58
Algorytm: A czy da się to zrobić algebraicznie, a nie za pomocą rysunku? Bo |DC| wychodzi mi √1852
xd
11 kwi 23:59
chichi:
A czy sposób z
23:38 nie jest algebraiczny?
12 kwi 00:08
I'm back:
Cholera... Podałem chyba Najprostrzy algebraiczny sposób, a Ty nie dość że z Gdańska do Sopotu
przez Kraków chcesz jechać, to jeszcze narzekasz ze za dużo paliwa spalisz.
12 kwi 00:18
Mila:
Algorytm podaj całą treść zadania, bo z Twoich dopisków to tylko jest mętlik .
12 kwi 16:56
Pr713: Też się z tym zgodzę.
12 kwi 22:15
Mila:
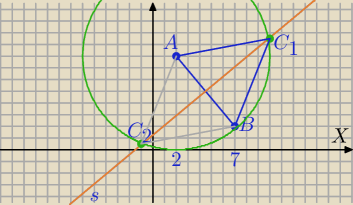
"Dany jest trójkąt równoramienny ABC o podstawie AB i ramionach długości 8. Znając współrzędne
pkt A(2,8) oraz B(7,2) oblicz współrzędne pkt C, który leży na pierwszej połowie układu
współrzędnych"
1) Symetralna AB:
(x−2)
2+(y−8)
2=((x−7)
2+(y−2)
2
2) Okrąg ośrodku B i promieniu r=8
(x−7)
2+(y−2)
2=64
C− Punkt przecięcia tego okręgu i symetralnej AB
| | 5 | | 5 | |
(x−7)2+( |
| x+ |
| −2)2=64 |
| | 6 | | 4 | |
licz dalej sam.
Czy dobrze przepisałeś dane w zadaniu?
Nieprzyjazne rachunki.
12 kwi 22:24