Dowód geometryczny Vateusz: Ramię AD trapezu ABCD (w którym AB II CD) przedłużono do punktu. E takiego, że AE = 3 · AD. Punkt M leży na podstawie AB oraz MB = 4 · AM. odcinek ME przecina przekątną BD w punkcie P . Udowodnij że |PB| = 6 |PD| Przeprowadzam dowód następująco : |PB| / |DB| = 4/5 |PB| + |PD| = |DB| |PB| / |PB|+|PD| = 4/5 5|PB| = 4|PB| + 4|PD| 4|PD| = |PB| A ma wyjść, że równa się 6 zamiast 4 Będę wdzięczny za pomoc

I'm back: Błąd już w pierwszej linijce dowodu.

	6
|PB| =		|DB|
	7

I'm back: A sorki − − − to masz udowodnić

I'm back: No to w takim razie − skąd pierwsza linijka

Vateusz: Dlaczego ? Z czego to wynika ?

Vateusz: Pierwsza linijka faktycznie jest źle teraz zauważyłem. Myślałem, że DBA i PBM są podobne, ale teraz widzę że jednak nie.

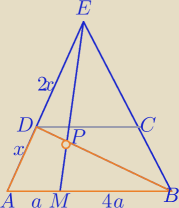
Mila: Skorzystaj z tw. Menelausa. ΔABD przecięto prostą EM.

BM		AE		DP
	*		*		=1⇔
MA		DA		PB

4a		3x		DP
	*		*		=1
a		2x		PB

4		3		DP
	*		*		=1⇔
1		2		PB

DP		1
	=		⇔
PB		6

|PB|=6|PD| cnw

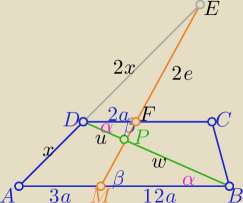
Eta: ΔAME ∼ΔDFE z cechy (kkk) w skali s=3/2 to |DF|= 2a

	12a
i ΔMBP ∼ ΔDFP z cechy (kkk) w skali k=		=6
	2a

	w
to		=k=6
	u

|PB|=6|PD| c.n.w. i po ptokach