Równoliczność zbiorów marność: Zadanie 8. Czy zbiory A i B: a) A = N, B = {2n, n ∈ N} b) A = (a, b), B = (c, d) ⊆ R oraz B = [c, d] ⊆ R c) A = (a, b), B = R d*) A = (0, 1), B = ((0, 1] × (0, 1]) \ {< 1, 1 >}, e*) A = ([0, 1] × [0, 1]), B = ((0, 1] × (0, 1]) \ {< 1, 1 >}. są równoliczne? a) f: A → B f(a) = 2a Funkcja f jest bijekcją, zatem zbiory są równoliczne Z kolejnymi podpunktami ma problem, dlatego prosiłbym o wskazówki

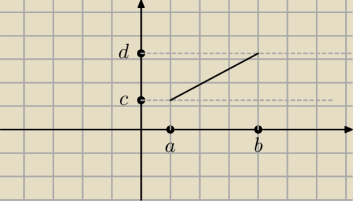
Maciess: b) funkcja liniowa jak na rysunku. Mozna tez powiedzieć, że każdy ten odcinek jest równoliczny z odcinkiem (0,1).

wredulus_pospolitus: a te z * to co to mają być? Dodatkowe podpunkty?

marność: To chyba są zadania o teoretycznie podwyższonym poziomie trudności

Maciess: c) w sumie tak samo. Oba równoliczne z (0,1). Możesz też użyć funkcji tg. Może powiedz jakie miałeś twierdzenia przedstawione i z czego można korzystać.

marność: Z tego działu miałem tylko przestrzeń ilorazową, zasadę abstrakcji i taką definicję relacji równoważności: N𝐢𝐞𝐜𝐡 ℛ będzie relacją 𝑨 do 𝑨. N𝐚𝐳𝐰𝐢𝐞𝐦𝐲 ℛ relacją równoważności na 𝑨, jeśli 𝒙ℛ𝒙 dla wszystkich 𝒙∈𝑨, 𝒙ℛ𝒚 implikuje, że 𝒚ℛ𝒙 dla wszystkich 𝒙,𝒚∈𝑨, 𝒙ℛ𝒚 i 𝒚ℛ𝒛 implikuje 𝒙ℛ𝒛 dla wszystkich 𝒙,𝒚,𝒛∈𝑨.

Maciess: Chyba coś zapomniałeś zanotowac XD Standardowa śpiewka. Zacznij do tej lektury. Guzicki − Wykłady ze wstępu do matematyki. Poczytaj, pooglądaj przykłady i wróć jak dalej będą pytania

marność: Tak zrobię, dziękuję za pomoc