Wzory Viete'a wyprowadzenie
Algorytm: Jak wyprowadzić |x1| + | x2| na wzory Viete'a? Czy można wytłumaczyć szczegołnie dlaczego jest
−2|x1x2|?
6 kwi 23:16
Algorytm: Znaczy +2|x1x2|*
6 kwi 23:18
123:
ze wzoru
a2+b2= (a+b)2−2ab
6 kwi 23:23
Algorytm: Ale no ja wiem, że |x1| to √x12 i |x2| to √x22 i że później jest √x12 + x22 i później
mamy
√(x1+x2)2 − 2x1x2. ALE poza tym, co ja napisałem musi dodatkowo jeszcze być + 2|x1*x2|.
Dlaczego?
6 kwi 23:40
123:
|x1|+|x2| = s >0
x12+x22+2|x1|*|x2| = (x1+x2)2−2x1*x2+2|x1*x2|
7 kwi 00:12
Algorytm: Ale czym jest to "s > 0"? I jak się pojawiło 2|x1x2|
7 kwi 02:24
7 kwi 18:16
ite:
Masz obliczyć sumę |x1| + |x2|, wykorzystując wzory Viete'a.
Najłatwiej zacząć od obliczenia:
(|x1| + |x2|)2 = |x1|2 + 2|x1|*|x2| + |x2|2 // korzystam ze wzorów skróconego
mnożenia
ponieważ |x1|2 = x12 mogę zapisać
|x1|2 + 2|x1|*|x2| + |x2|2 = x12 + 2|x1|*|x2| + x22 = x12 + x22 + 2|x1|*|x2|
skoro x12 + x22 = (x1 + x2)2 − 2x1*x2 więc
x12 + x22 + 2|x1|*|x2| = (x1 + x2)2 − 2x1*x2 + 2|x1*x2|
7 kwi 18:34
xxx:
|x1| + |x2| = √ (ba)2 − 2ca + 2|ca|
7 kwi 20:02
Algorytm: @ite , okej rozumiem, że możemy to spotęgować, ale dlaczego nie mogę od razu potraktować |x1|
jako √x21 i tak samo z |x2| i później dać ich pod jeden pierwiastek i skorzystać ze wzoru
skróconego mnożenia? dlaczego +2|x1x2| jest obowiązkowe?
7 kwi 20:52
ite:
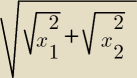
"dlaczego nie mogę od razu potraktować |x
1| jako
√x12 i tak samo z |x
2| i później dać ich
pod jeden pierwiastek"
Otrzymasz coś takiego jak na rysunku i nie będzie jak sensownie skorzystać ze wzoru skróconego
mnożenia.
7 kwi 22:33
Algorytm: Niestety nadal nie rozumiem

Skąd jest ten drugi pierwiastek?
Czy |x
1|+|x
2| nie jest to same co
√x12 + x22 ?
7 kwi 23:57
Eta:
|x1|+|x2| = t >0
podnosimy obustronnie do kwadratu
|x1|2+2|x1|*|x2|+|x2|2 = t2 i |x1|2+|x2|2=x12+x22
x12+x22 +2|x1*x2|=t2
(x1+x2)2−2x1*x2+2|x1*x2|=t2
to
|x1|+|x2|= t=√(x1+x2)2−2x1*x2+2|x1*x2| = √(ba)2−ca+2*|ca|
czy teraz już jasne ?
8 kwi 00:33
Eta:
Czy taka równość zachodzi ?
√a2+b2 = √a2+√b2 −− nie zachodzi !
a Ty piszesz,że
|x1|+|x2|= √x12+x22 −−−− nonsens ! nie zachodzi! jak wyżej
to tak jakbyś liczył ,że :
√36+25= 6+5 ?
8 kwi 00:39
Eta:
To ja się opisałam
a ten "zwinął " się i ..........

8 kwi 00:45


 ?
?
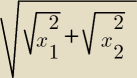 "dlaczego nie mogę od razu potraktować |x1| jako √x12 i tak samo z |x2| i później dać ich
pod jeden pierwiastek"
Otrzymasz coś takiego jak na rysunku i nie będzie jak sensownie skorzystać ze wzoru skróconego
mnożenia.
"dlaczego nie mogę od razu potraktować |x1| jako √x12 i tak samo z |x2| i później dać ich
pod jeden pierwiastek"
Otrzymasz coś takiego jak na rysunku i nie będzie jak sensownie skorzystać ze wzoru skróconego
mnożenia.
 Skąd jest ten drugi pierwiastek?
Czy |x1|+|x2| nie jest to same co √x12 + x22 ?
Skąd jest ten drugi pierwiastek?
Czy |x1|+|x2| nie jest to same co √x12 + x22 ?
