równanie okręgu
anonim123: wyznacz równanie okręgu wpisanego w trójkąt o bokach zawartych w prostych x=4, 3x−4y+36=0,
4x+3y+23=0
6 kwi 12:30
kotek:
o: (x+1)2+(y−2)2=25
================
6 kwi 13:25
anonim123: A można prosić o rozwiązanie?
6 kwi 13:34
chichi:
Jakie są dwie ostatnie proste względem siebie?

6 kwi 13:37
kotek:
⊥

6 kwi 13:40
chichi:
No to zadanie już praktycznie rozwiązane, może autorka w końcu się wysili? Całe życie
gotowce...
6 kwi 13:41
janek191:
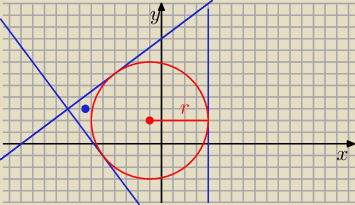
6 kwi 15:54
anonim123: Dziękuję

6 kwi 17:49
Mariusz:
anonim masz trzy równania prostych
Pamiętasz konstrukcję dwusiecznej
Masz dane równania prostych zawierających ramiona kąta
1. Wybierasz równania dwóch prostych i rozwiązujesz układ równań
aby otrzymać współrzędne wierzchołka kąta
2. Na jednym z ramion kąta obierasz sobie punkt D
(punkt D obierasz sobie dowolnie na ramieniu kąta
aczkolwiek jest to punkt różny od B)
3. Piszesz równanie okręgu o środku w punkcie B i promieniu BD
4. Niech punkt E będzie przecięciem okręgu i prostej zawierającej drugie ramię kąta
(to ramie na którym nie leży punkt D)
Tutaj rozwiązujesz układ równań w którym jedno równanie jest równaniem okręgu z punktu 3.
a drugim równaniem jest równanie ogólne prostej zawierającej drugie ramię kąta
W tym punkcie dostaniesz dwa punkty E które dadzą dwie wzajemnie prostopadłe proste
dla każdego dzielonego kąta więc musisz poprawnie wybrać punkt E
5. Piszesz równanie prostej przechodzącej przez punkty D oraz E
6. Piszesz równanie prostej prostopadłej do prostej DE oraz przechodzącej przez punkt B
Powyższe kroki przeprowadzasz dla dwóch wybranych kątów otrzymując
równania dwusiecznych dwóch kątów
Rozwiązujesz układ równań i dostajesz współrzędne punktu S
będącego środkiem okręgu wpisanego
Co do promienia to też można go znaleźć sposobem konstrukcyjnym
Piszesz równanie prostej prostopadłej do prostej zawierającej wybrany bok trójkąta
i przechodzącej przez środek okręgu wpisanego
Rozwiązujesz układ równań i dostajesz punkt F
Liczysz odległość SF
Tutaj jedyne czego nie napisałem to sposób wyboru punktu E
w 4. kroku wyznaczania równania dwusiecznej
6 kwi 19:10
Mariusz:
Kotek podejrzanie ładnie wygląda to równanie okręgu
Zwykle pierwiastki wychodzą
A chichi jak zwykle się mądrzy a nic sensownego nie napisał
6 kwi 19:20
chichi:
A co ja jestem maszyna do pisania rozwiązań czy co?

Jak będę chciał to napisze rozwiązanie, jak nie to nie...
6 kwi 19:33
Min. Edukacji: Chi Chi dobrze gada

6 kwi 19:54
Mariusz:
"Chichi dobrze gada" ta tylko co on takiego napisał co pomogłoby
użytkownikowi anonim napisać równanie tego okręgu
No tak spamerów takich jak chichi i ten Min. Edukacji nie cenzorują
a kerajsa który przynajmniej stara się sensownie odpowiadać już tak
To pogarsza jakość tego forum
6 kwi 20:01
janek191:
Np.
4 x + 3 y + 23 = 0
x = 4
−−−−−−−−−−−−−−
Otrzymujemy:
x = 4 y = −13
A=(4. −13)
========
3 x − 4 y + 36 = 0
x = 4
−−−−−−−
Otrzymujemy
x = 4 y =12
B = ( 4, 12 )
=========
3 x − 4y+36 = 0 / * 4
4 x + 3y + 23 = 0 / * 3
−−−−−−−−−−−−
12 x − 16 y + 144 = 0
12 x + 9 y + 69 = 0
−−−−−−−−−−− odejmujemy stronami
25 y = 75
y = 3
====
więc x = − 8
=========
C = ( − 8, 3)
=============
zatem
I AB I = 12 − (−13) = 25
I AC I =
√(−12)2 + 162 =
√400 = 20
I BC I =
√(−12)2 + (−9)2 =
√225 = 15
P = 0,5*20*15 = 150
więc
Niech S = ( a, b)
więc odległości od prostych są równe
| I 3 a − 4 b + 36 I | |
| = r = 5 |
| √32 +(−4)2 | |
oraz
| I 4 a + 3 b + 23 I | |
| = r = 5 |
| √42 +32 | |
czyli
I 3 a − 4 b + 36 I = 25
I 4 a + 3 b + 23 I = 25
−−−−−−−−−−−−−−−−−−−−−
3a − 4 b = − 11 / * 4
4a + 3 b = 2 / * 3
−−−−−−−−−−−−−−−
12 a − 16 b = − 44
12 a + 9 b = 6
−−−−−−−−−−−−
25 b = 50
b = 2
zatem
a = − 1 oraz S = ( − 1, 2)
Równanie okręgu wpisanego:
( x + 1)
2 = ( y − 2)
2 = 5
2
======================
6 kwi 20:07
janek191:
Poprawka:
( x + 1)2 + ( y − 2)2 = 25
6 kwi 20:12
kotek:
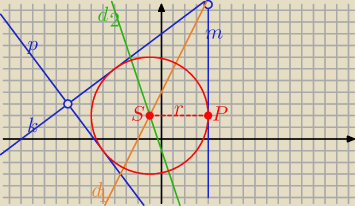
Piszemy równanie dwusiecznej kąta wewnętrznego:
d
1 : |3x−4y+36|=5|x−4| ⇒ 3x−4y+36= −5x+20 ⇒ y=2x+4
d
2 : |4x+3y+23|=5|x−4| ⇒ 4x+3y+23= −5x+20 ⇒ y= −3x−1
S= d
1∩d
2 : 2x+4= −3x−1 ⇒ x=−1 i y= 2 to S=(−1,2)
P=(4,2)
r =|SP|= 5
o : (x+1)
2+(y−2)
2=25
=================
6 kwi 20:26
Mariusz:
kotek a dlaczego po opuszczeniu tej wartości bezwzględnej po prawej stronie
wziąłeś(aś) wartość z minusem w obydwu przypadkach
kotek tak zgadza się ja podałem sposób oparty o konstrukcję dwusiecznej
który może i jest dłuższy ale łatwiej na niego wpaść o ile pamiętamy konstrukcję dwusiecznej
Kotek mimo iż sposób przez ciebie przedstawiony jest nieco krótszy od sposobu konstrukcyjnego
to i tak w nim też musimy wybierać równanie dwusiecznej
Jest jednak sposób na równanie dwusiecznej który nie wymaga wyboru jednej
z dwóch wzajemnie prostopadłych prostych dla każdego dzielonego kąta
6 kwi 23:14
Mila:
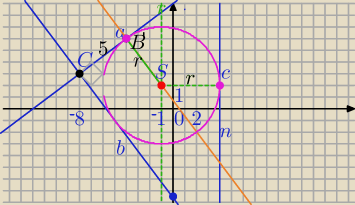
1)
Wykorzystuję prostopadłość prostych:
a: 3x−4y+36=0
b: 4x+3y+23=0
k⊥m, n⊥OX
2) Obliczenia u
Janka
C=(−8,3) , B=(4,12),A=(4,−13)
|AC|=20, |BC|=15, |AB|=20
3)
a+b=2r+2R
15+20=2r+25
r=5, r⊥n w punkcie styczności
S leży na prostej x=−1
4) Kreślę prostą równoległą do AC ( b) odległą od niej o 5.
CB
→[12, 9] |CB|=15
| | 1 | |
|CB'|=5 ⇔CB= |
| *[12,9]=[4,3] |
| | 3 | |
B'=(−8+4,3+3)=(−4,6)
b': 4x+3y+C'=0 i B'∊b'⇔
−16+18+C'=0, C'=(−2)
b' : 4x+3y−2=0
| | 4 | | 2 | | 4 | | 2 | |
y=− |
| x+ |
| , y=− |
| *(−1)+ |
| =2 |
| | 3 | | 3 | | 3 | | 3 | |
S=(−1,2) − punkt przecięcia prostych : x=−1, 4x+3y−2=0
5)Równanie okręgu:
(x+1)
2+(y−2)
2=25
===============
8 kwi 20:16
Mariusz:
Ale to nie będzie ogólne przy danych innych prostych już to nie zadziała
Sposób z przecięciem dwusiecznych do wyznaczenia środka jest ogólny
ale trzeba odpowiedzieć na pytanie jakie równanie prostej wybrać lub podać
sposób na równanie dwusiecznej który daje tylko jedną prostą
Zarówno sposób wynikający z konstrukcji dwusiecznej (ten który ja opisałem)
jak i sposób polegający na przyrównaniu odległości punktu od obydwu ramion kąta
(ten przedstawiony przez Kotek) dają dwie wzajemnie prostopadłe proste
dla każdego dzielonego kąta więc trzeba podać jak poprawnie wybrać równanie dwusiecznej
albo podać sposób na równanie dwusiecznej który dla każdego dzielonego kąta
daje tylko jedną prostą
Kotek jakoś nie odpowiedział na pytanie dlaczego akurat taką prostą wybrał
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Inaczej można by skorzystać z tego że szukany okrąg jest styczny do każdego z boków
więc mielibyśmy układ trzech równań kwadratowych powstały następująco
Piszemy równanie okręgu przyjmując za współrzędne środka i promienia jakieś nieznane wartości
Piszemy równanie prostej do której okrąg ma być styczny
Wyznaczamy jedną z niewiadomych (x bądź y) z równania prostej
i wstawiamy do równania okręgu a następnie liczymy wyróżnik tak powstałego równania
Wyróżnik ten przyrównujemy do zera i otrzymujemy równanie kwadratowe
Powyższe kroki wykonujemy dla każdej z podanych prostych
i dostaniemy układ trzech równań kwadratowych z trzema niewiadomymi
8 kwi 22:20
Mila:
Mariusz, w planimetrii nie działa się schematami, wykorzystuje się własności figur.
Czasem rozwiązanie jest proste, innym razem skomplikowane.
Czasem dużo rachunków , innym razem mało − w zależności od tego co zauważymy w danej chwili.
8 kwi 23:40
chichi:
Mariusz działa tylko i wyłącznie schematami...

8 kwi 23:48
Eta:

8 kwi 23:50
chichi:

8 kwi 23:59
Eta:
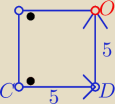
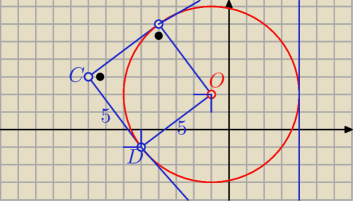
Jak wyżej C(−8,3) r=|CD|=|DO|=5
i z wektorów CD ⊥pr.CB to
→
CD= [3,−4] ⇒ D=(−8+3,3−4)= (−5,−1)
DO= [4,3] ⇒ O=(−5+4, −1+3) = (−1,2)
o: (x+1)
2+(y−2)
2=25
9 kwi 01:59
Eta:
9 kwi 02:07
Mariusz:
Mnie najbardziej podoba się rozwiązanie użytkownika kotek
jednak brakuje mi w nim następującej rzeczy
kotek napisał
"Piszemy równanie dwusiecznej kąta wewnętrznego:
d1 : |3x−4y+36|=5|x−4| ⇒ 3x−4y+36= −5x+20 ⇒ y=2x+4
d2 : |4x+3y+23|=5|x−4| ⇒ 4x+3y+23= −5x+20 ⇒ y= −3x−1"
No i skąd wiedział że po opuszczeniu wartości bezwzględnej po
prawej stronie równania należy zmienić znak
Kotek nie podał kiedy zmieniać znak po opuszczaniu wartości bezwzględnych
i to jest wielki minus jego rozwiązania poza tym jest ok
Ciekawe czemu uparł się na przyrównanie odległości punktu od ramion kąta
Na równanie dwusiecznej jest inny sposób który daje
tylko równanie dwusiecznej kąta wewnętrznego
9 kwi 07:09
Mila:
Mariusz, były już dwa rozwiązania, ponieważ nie wiedziałeś, którą dwusieczną wybrać
to napisałam rozwiązanie bez korzystania z dwusiecznej.
W każdym przypadku, możesz uniknąć z równań dwusiecznych ale trochę więcej jest obliczeń.
Jeżeli ustalasz długość promienia i dalej szukasz wsp. środka okręgu wpisanego,
to masz więcej obliczeń.
Przeanalizuj rozwiązanie z 20:26. To nie jest trudne, a sposób jest prosty.
9 kwi 14:42
Mila:
Poszukaj wzoru na współrzędne środka okręgu wpisanego w trójkąt,
jeśli znasz wsp. wierzchołka Δ. Jest na forum.
Długości boków i wsp. wierzchołków Δ są całkowite, 5 minut i masz rozwiązanie.
9 kwi 14:46
kotek:
@
Mariusz
Ja Twoich "trylogii" na temat rozwiązania banalnego zadania nie czytam
bo kotek jest leniwy

Narysowałam proste zawierające boki trójkąta
i wybrałam równania tych dwusiecznych, które przecinają się
we wenętrzu trójkąta
i po ptokach

Gdybyś uczył w szkole takimi "rozwlekłymi" metodami
to lekcja musiałaby trwać co najmniej 180 min
Pozdrawiam

9 kwi 14:56
Mariusz:
Mila widziałem ten wzór ale koleś podał go bez uzasadnienia
Nawet nie wiadomo czy jest prawdziwy
Znam sposób na równanie dwusiecznej który daje tylko dwusieczną kąta wewnętrznego
i bynajmniej nie poznałem go na forach internetowych
Jeżeli chodzi o wybór dwusiecznej dla przedstawionego przeze mnie sposobu bazującego
na konstrukcji dwusiecznej to poznałem go na anglojęzycznym forum
jednak chciałem abyście wy go podali
Kotek bez warunku na wybór dwusiecznej twoje rozwiązanie jest bezużyteczne
Można wybrać tę dwusieczną bez rysowania
Sposób który podałem może i jest trochę dłuższy od tego co ty podałaś
ale łatwo na niego wpaść znając konstrukcję dwusiecznej
Programu do rysowania okręgu wpisanego w trójkąt raczej byś nie napisała
ani nawet takiego który by wypisywał na ekran to rozwiązanie
To zadanie programistyczne też jest banalne ale aby program dobrze
działał byś musiała oprogramować sposób na równanie dwusiecznej który daje
tylko równanie dwusiecznej kąta wewnętrznego
albo przynajmniej oprogramować sposób wyboru dwusiecznej
Tak z ciekawości Kotek = Eta ?
9 kwi 17:53
Mila:
Mariusz −Napiszę wyprowadzenie wzoru, ale nie dzisiaj.
9 kwi 20:10
Pr713: Przejdź może @Mariusz na inne forum jak tutaj Ci się nudzi
10 kwi 14:59
Mariusz:
Powiedział co wiedział
(przy czym powiedział to tak dla rymu bo tak stricte powinno być napisał)
Mila istnieje sposób na wyprowadzenie tego wzorku na
współrzędne środka okręgu wpisanego bez korzystania z równania dwusiecznych
Gdybyśmy zmodyfikowali to zadanie w następujący sposób
Wyznacz równanie okręgu wpisanego w trójkąt o bokach zawartych w prostych
a1x+b1y+c1=0 , a2x+b2y+c2=0, a3x+b3y+c3=0
przy założeniu że te proste są parami nierównoległe
to jak byście to zadanie rozwiązali ?
Spróbuję teraz napisać dlaczego sposób konstrukcyjny działa
Masz dane równania prostych zawierających ramiona kąta
Sposób konstrukcyjny wariant I
1. Wybierasz równania dwóch prostych i rozwiązujesz układ równań
aby otrzymać współrzędne wierzchołka kąta
2. Na jednym z ramion kąta obierasz sobie punkt D
(punkt D obierasz sobie dowolnie na ramieniu kąta
aczkolwiek jest to punkt różny od B)
3. Piszesz równanie okręgu o środku w punkcie B i promieniu BD
4. Niech punkt E będzie przecięciem okręgu i prostej zawierającej drugie ramię kąta
(to ramie na którym nie leży punkt D)
Tutaj rozwiązujesz układ równań w którym jedno równanie jest równaniem okręgu z punktu 3.
a drugim równaniem jest równanie ogólne prostej zawierającej drugie ramię kąta
W tym punkcie dostaniesz dwa punkty E które dadzą dwie wzajemnie prostopadłe proste
dla każdego dzielonego kąta więc musisz poprawnie wybrać punkt E
5. Piszesz równanie prostej przechodzącej przez punkty D oraz E
6. Piszesz równanie prostej prostopadłej do prostej DE oraz przechodzącej przez punkt B
Otóż sposób ten działa bo konstruujemy tutaj trójkąt równoramienny w którym
prosta prostopadła do prostej zawierającej podstawę tego trójkąta i naprzeciwległy wierzchołek
dzieli ten trójkąt równoramienny na dwa przystające trójkąty prostokątne
Sposób konstrukcyjny wariant II
1. Wybierasz równania dwóch prostych i rozwiązujesz układ równań
aby otrzymać współrzędne wierzchołka kąta
2. Na jednym z ramion kąta obierasz sobie punkt D
(punkt D obierasz sobie dowolnie na ramieniu kąta
aczkolwiek jest to punkt różny od B)
3. Piszesz równanie okręgu o środku w punkcie B i promieniu BD
4. Niech punkt E będzie przecięciem okręgu i prostej zawierającej drugie ramię kąta
(to ramie na którym nie leży punkt D)
Tutaj rozwiązujesz układ równań w którym jedno równanie jest równaniem okręgu z punktu 3.
a drugim równaniem jest równanie ogólne prostej zawierającej drugie ramię kąta
W tym punkcie dostaniesz dwa punkty E
Punkt E wybierasz tak aby ∡DEC był kątem wpisanym opartym na tym samym łuku
co kąt ∡DBC
(przy założeniu że punkt B jest wierzchołkiem dzielonego kąta
a punkt D leży na tej samej prostej co A)
5. Piszesz równanie prostej przechodzącej przez punkty D oraz E
6. Piszesz równanie prostej równoległej do DE i przechodzącej przez punkt B
Tutaj korzystamy z twierdzenia o kątach wpisanym i środkowym opartych
na tym samym łuku
Korzystamy też z tego że jeśli prostą przetniemy dwiema równoległymi do siebie prostymi
to odpowiednie kąty będą miały równe miary
Jeżeli będziemy umieli wybrać punkt E w kroku 4.
tak aby ∡DEC był kątem wpisanym opartym na tym samym łuku co kąt ∡DBC
to poradzimy sobie zarówno z wariantem I jak i z wariantem II
Sposób przedstawiony przez użytkownika Kotek może i jest szybszy
ale to czy po opuszczaniu wartości bezwzględnej zmieniamy znak
nie jest już takie oczywiste
Istnieje jeszcze sposób w którym równanie dwusiecznej otrzymujemy jednoznacznie
tzn nie musimy w nim wybierać prostej zawierającej dwusieczną kąta wewnętrznego
ale skoro wy nie chcecie go pokazać to i ja go nie pokażę
11 kwi 06:45
Mariusz:
Oj tutaj mały błędzik w oznaczeniu kątów otóż
Z układu równań w kroku 4.
dostajemy dwa punkty E oraz E'
I teraz punkt E wybieramy tak aby kąt ∡DEE'
był kątem wpisanym opartym na tym samym łuku co kąt środkowy ∡DBE'
W wariancie I punkt E odrzucamy a zostawiamy punkt E'
a w wariancie II punkt E zostawiamy a odrzucamy punkt E'
Kąty ∡DEC oraz ∡DBC mają taką samą miarę co kąty ∡DEE' oraz ∡DBE'
ale mogą nie być oparte na tym samym łuku
11 kwi 08:18
pr713: Nie widzisz, że nikogo to nie interesuje?
11 kwi 21:07
pr713: Jeszcze piszesz takie referaty o 6 rano...
11 kwi 21:07
janek191:
Pewnie nie może spać

?
11 kwi 21:08
pr713: Najwidoczniej

11 kwi 21:09
chichi:
Nie używaj "

" bo jeszcze pomyśli, że to ja mu tu wypominam, ale słusznie mnie również to nie
interesuje

11 kwi 21:24
Mariusz:
Mila napisała że wyprowadzi ten wzór na środek okręgu wpisanego bez dwusiecznych
ale jakoś nie odpowiada
", ale słusznie mnie również to nie interesuje"
To po co odpisujesz
Zresztą i tak nic sensownego tutaj nie napisałeś
Rozwiązanie przedstawione przez Kotek byłoby dobre
gdyby pokazała kiedy zmieniać znak przy opuszczaniu wartości bezwzględnej
12 kwi 08:31
Pr713: To czekaj dalej

13 kwi 12:15
anonim123: Skąd u janek191 duże P i obliczenie r?
14 kwi 22:07
anonim123: Już znalazłam na internecie ten wzór
14 kwi 22:28
Mariusz:
"To czekaj dalej "
No właśnie to pokazuje ile warte są zdania napisane przez Milę
anonim to jest wzór na pole powierzchni trójkąta
Ten wzór akurat bardzo łatwo wyprowadzić
ale oni i tak ci nie napiszą tego bo jedyne co umieją to tylko spamować
Jak go wyprowadzić − otóż dzielisz trójkąt na trzy mniejsze w ten sposób aby
promień okręgu wpisanego był wysokością każdego z tych trzech mniejszych trójkątów
a następnie liczysz sumę tych trzech trójkątów na które podzieliłaś wyjściowy trójkąt
15 kwi 09:44
Mariusz:
* sumę pól powierzchni , tego mi tutaj zabrakło
15 kwi 09:46
anonim123: Dziękuję😏
15 kwi 17:32
Mila:
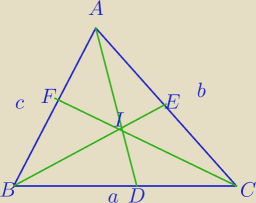 Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
A=(x
1,y
1), B=(x
2,y
2), C=(x
3,y
3}
I=(x
s,y
s)
1)
Współrzędne punktu D=(d1,d2).
2)
Współrzędne punktu I=(xs,ys)
======================
15 kwi 22:29
;): | | AS | |
Zastanawiam się skąd się wzięła zależność z 22:28 ( tutaj: |
| chyba chodziło o AI a nie |
| | AB | |
AS względem oznaczeń)
I skąd wiemy że to się równa skali tak samo jak reszta ilorazów? Tak samo nie rozumiem skąd się
wzięła zależność 2) z dwusiecznych, bo 1) to z twierdzenia dwusiecznej.
Tak samo współrzędna x
s = ...
15 kwi 23:49
;): Mogłabyś wytłumaczyć też dlaczego raz piszesz że xs = ...*x2 a potem *d1? Jedno to
współrzędna punktu B a drugie to D
16 kwi 00:09
Mila:
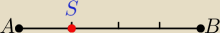
Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
Wiadomości:
1)
Podział odcinka AB w danym stosunku:
A =(x
1, y
1)
B=(x
2, y
2)
liczba k>0 (dodatnia),
Współrzędne : S(x
s,y
s)
x
s = (x
1 + k*x
2)/(1 + k)
y
s = (y
1+ k*y
2)/(1 + k)
16 kwi 00:14
Mila:
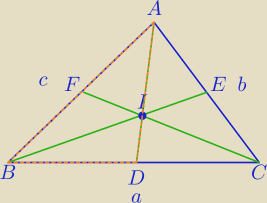
2)
a)
b)
W ΔADB −BI jest dwusieczną kąta B
| | BD | | DI | |
stąd |
| = |
| obliczymy BD z ΔBCA z tw (1) |
| | c | | AI | |
16 kwi 00:40
;): | | AS | | AI | |
To to okej, |
| = k, ale dlaczego też |
| = k jeśli dlatego że patrzymy na mały |
| | SB | | ID | |
| | b+c | |
trójkąt BDA i podział AD przez dwusieczną to ok, ale skąd ta proporcja |
| |
| | a | |
16 kwi 00:40
;): Dalej, skąd się bierze zależności na xs? Licznik jest dla mnie w miarę jasny, mianownik nie
16 kwi 00:41
Mila:
Może jutro wyjaśnię

Dobranoc.
16 kwi 00:43
;): | | ac | |
Teraz wszystko rozumiem w twoim poście 00:40 oprócz przejścia BD = |
| , Akurat piszesz |
| | ... | |
to do czego doszedłem sam 😂
16 kwi 00:48
;): Dobranoc
16 kwi 00:48
;): obliczymy BD z ΔBCA z tw (1) − tutaj dalej za bardzo nie rozumiem skąd − CF jako dwusieczna?
Ta skala k to jest stosunek przecięcia się dwusiecznych? Skąd wiemy że jest on równy?
16 kwi 23:50
chichi:
A dlaczego piszesz pod innym nickiem?

17 kwi 11:35
;): Czasami tak lubię
17 kwi 17:04
;): Swoją drogą, pewnie sam się podłączasz pod moje pytanie

17 kwi 17:21
circle:
Masz narysowane dwusieczne 3 kątów Δ.
BE jest dwusieczną kąta B w ΔABC , zatem CI jest dwusieczną kąta B w ΔABD.
Z tw. o dwusiecznej kąta mamy :
17 kwi 17:28
chichi:
Nigdzie się nie podłączam

17 kwi 17:57
Mila:

17 kwi 18:09
Mariusz:
Milu chciałbym ci podziękować po pierwsze za to że pokazałaś jak wyprowadzić
ten wzorek na współrzędne środka okręgu wpisanego a po wtóre (nawet ważniejsze)
za to że dowiodłaś iż dotrzymujesz obietnic − że twoje słowa coś znaczą
A ja niepotrzebnie dałem się sprowokować tym osobom co nic nie wnieśli do tematu
i stąd zbyt pochopny osąd
Wszystkiego najlepszego
17 kwi 18:16
Mila:

Wybaczam.
17 kwi 18:23
;): | | ac | |
@circle napisałeś dosłownie to samo co Mila, a skąd się wzięła zależność BD = |
| . |
| | b+c | |
| | ID | | BD | | BD | | c | |
Mamy na razie |
| = |
| oraz |
| = |
| . Miałeś na myśli z dwusiecznych BI |
| | AI | | c | | DC | | b | |
i CI? Jak możesz to rozpisz, no i jeszcze dlaczego w x
s w mianowniku jest 1+k

18 kwi 08:48
Mariusz:
1. Wybierasz równania dwóch prostych i rozwiązujesz układ równań
aby otrzymać współrzędne wierzchołka kąta
2. Na jednym z ramion kąta obierasz sobie punkt D
(punkt D obierasz sobie dowolnie na ramieniu kąta
aczkolwiek jest to punkt różny od B)
3. Piszesz równanie okręgu o środku w punkcie B i promieniu BD
4. Niech punkt E będzie przecięciem okręgu i prostej zawierającej drugie ramię kąta
(to ramie na którym nie leży punkt D)
Tutaj rozwiązujesz układ równań w którym jedno równanie jest równaniem okręgu z punktu 3.
a drugim równaniem jest równanie ogólne prostej zawierającej drugie ramię kąta
W tym punkcie dostaniesz dwa punkty E które dadzą dwie wzajemnie prostopadłe proste
dla każdego dzielonego kąta więc musisz poprawnie wybrać punkt E
5. Piszesz równanie prostej przechodzącej przez punkty D oraz E
6. Piszesz równanie prostej prostopadłej do prostej DE oraz przechodzącej przez punkt B
Jeżeli chodzi o powyższy sposób konstrukcyjny znajdowania równania dwusiecznej to sam pomysł
z trójkątem równoramiennym dzielonym na dwa przystające trójkąty prostokątne jest dobry
Problemem jest to że do układu równań z kroku 4. wziąłem równanie prostej
a ramię kąta jest półprostą i stąd jedno dodatkowe równanie
Gdybyśmy znaleźli inny sposób na uzyskanie trójkąta równoramiennego
niż rozwiązanie tego układu równań z okręgiem i prostą to moglibyśmy
dostać równanie dwusiecznej tylko kąta wewnętrznego
Czego możemy użyć aby znaleźć współrzędne wierzchołków tego trójkąta równoramiennego ?
Wierzchołki te powinny leżeć na ramionach kąta więc układ równań z okręgiem i prostą
tutaj nie pasuje
18 kwi 15:10
Mila:
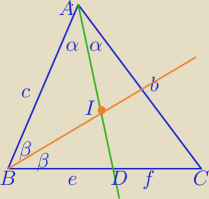
1)
W ΔABC: Z tw. o dwusiecznej kąta A
2) W ΔABD:
Z tw. o dwusiecznej kąta B
| AI | | b+c | |
| = |
| =k w takim stosunku jest podzielony odcinek AD |
| ID | | a | |
3) Dalej z wzoru na współrzędne I(x
s,y
s)
A=(x
1,y
1), D=(d
1,d
2)
| | | |
xs= |
| ⇔ mnożę licznik i mianownik przez a |
| | | |
dalej wiadomo?
Mam nadzieję, że nie ma literówek.
18 kwi 17:38
Mariusz:
Co do równania dwusiecznej to problemów z wyborem równania nie będzie jeżeli do
znalezienia wierzchołków trójkąta równoramiennego
dzielonego na dwa przystające trójkąty prostokątne użyjemy wektorów
Mila całkiem niezły sposób pokazujący że do znalezienia współrzędnych środka okręgu wpisanego
nie trzeba znać równań dwusiecznych
18 kwi 18:28
:) : Mila, już zrozumiałem prawie wszystko oprócz "wzoru" na x
s . Rozumiem że w liczniku mamy x
1 +
k*d
1,
| | AI | |
bo |
| = k ⇒ AI = k*ID, tak? Ale mianownika kompletnie |
| | ID | |
19 kwi 12:19
:) : "dalej wiadomo?" − tak

19 kwi 12:19
:): Odnośnie tego wzoru na xs, jeśli mamy AS /SD = 3 = k oraz xA = 1, xD = 4 ( już wiemy że
xs = 3)
To ze wzoru mamy xs = (1+3*4)/(1+3) = 13/4 a nie 3
19 kwi 12:48
:): Dobra usuń Mila moje posty oprócz drugiego, już ogarnąłem, a żeby nie było bałaganu, x
s =
3,25

Wszystko jasne dzięki <3
19 kwi 13:06
daras: @
Mila usuń wszystkie posty od początku tego forum i...
postaw go na nowo

co Ty na to?
19 kwi 14:40
:): Miałem na myśli 3 posty...
19 kwi 16:06
Mila:
Ad
16:06 musisz napisać z której godziny usunąć wpisy, w tym wątku jest taki bałagan, że
mogłabym
usunąć nie to, co chciałbyś.
daras lubię Twoje poczucie humoru

19 kwi 16:59
:): Jak chcesz to proszę usuń np ostatnie 5
19 kwi 17:11
:): | | BD | |
Mam tylko jeszcze pytanie odnośnie tego czy na pewno |
| = k? 15 kwietnia 22:29 |
| | DC | |
| | AI | |
Natomiast odnośnie 18 kwietnia 17:38 |
| że to równa się k to okej, bo takie daliśmy |
| | ID | |
założenie, że AD jest podzielony w skali k, ale co do BD i DC nie mogę znaleźć uzasadnienia
19 kwi 17:16
:): Czy tam po prostu niepotrzebnie to dopisałaś? Bo w sumie to że BD do DC jeśli by się równało
skali k to i tak to chyba nie jest przydatne
19 kwi 17:18
Mila:
ad. 17:18
Potrzebne w dowodzie do ustalenia współrzędnych punktu D, które wykorzystuje się do ustalenia
współrzędnych środka okręgu wpisanego w podany trójkąt.
19 kwi 22:30
Mariusz:
A przede wszystkim usuń darasa albo pokaż choć jeden wątek w którym pomógł
19 kwi 23:52
daras: @ Mariuszku take it easy !
zawsze jesteś niesprawiedliwy, to pewnie wina twojego ego
lepiej załóż okulary
20 kwi 08:49
kerajs:
''Mariusz: (...) pokaż choć jeden wątek w którym pomógł''
Zdefiniuj co to znaczy ''pomógł'', a ja wskażę wątek.
20 kwi 14:07
Mariusz:
Milu dobrze że pokazałaś jak znaleźć ten środek okręgu
Uniezależniłaś w ten sposób rozwiązanie od danych konkretnych równań prostych
tzn rozwiązanie będzie nadal poprawne gdy zmienimy równania tych prostych
(byleby nie były parami równoległe)
Rozwiązanie użytkownika kotek jest niepełne bo nie chciała odpowiedzieć
nam na pytanie kiedy zmieniać znak przy opuszczaniu wartości bezwzględnych
w równaniu dwusiecznej
(Jeżeli wykorzystamy ten sam pomysł co w podejściu konstrukcyjnym
ale rachunki będziemy wykonywać na wektorach to nie będzie problemów z
wyborem równania dwusiecznej)
20 kwi 15:36
:): @Mila ad 22:30
To skąd wiemy że punkt D dzieli odcinek AC w takim samym stosunku jak punkt I odcinek AD?
20 kwi 18:41
:): | | c | | e | |
Przecież jeśli |
| = |
| = k |
| | b | | f | |
| | c | | b | | AI | | c | |
To cf = be, ale |
| = |
| = |
| , a |
| ≠ k |
| | e | | f | | ID | | e | |
20 kwi 18:45
:): Czy to jest aby na pewno podział w tej samej skali k? Czy nie są to dwie różne skale k1 i k2?
20 kwi 18:46
Mariusz:
Milu podpowiedziałabyś jak uprościć rozwiązanie następującego układu równań
(z samym rozwiązaniem nie powinno być problemu jeśli znamy
podstawy rachunku macierzowego − wyznaczniki lub macierz odwrotna i mnożenie)
((xA − xB)b − (xA − xC)c)x − ((yB − yA)b − (yC − yA)c)y =
xA((xA − xB)b − (xA − xC)c) − yA((yB − yA)b − (yC − yA)c)
((xA − xB)a + (xB − xC)c)x − ((yB − yA)a + (yC − yB)c)y =
xB((xA − xB)a + (xB − xC)c) − yB((yB − yA)a + (yC − yB)c)
Powyższe równania otrzymałem ze sposobu konstrukcji dwusiecznej
ale nie mam pomysłu na uproszczenie rozwiązania tego układu
Jeżeli wklepiecie sobie te równania do Geogebry to z dokładnością do błędu numerycznego
pokaże wam że te równania rzeczywiście są równaniami dwusiecznych
(kąta przy wierzchołku A oraz kąta przy wierzchołku B)
4 maj 15:52




 Jak będę chciał to napisze rozwiązanie, jak nie to nie...
Jak będę chciał to napisze rozwiązanie, jak nie to nie...

 Piszemy równanie dwusiecznej kąta wewnętrznego:
d1 : |3x−4y+36|=5|x−4| ⇒ 3x−4y+36= −5x+20 ⇒ y=2x+4
d2 : |4x+3y+23|=5|x−4| ⇒ 4x+3y+23= −5x+20 ⇒ y= −3x−1
S= d1∩d2 : 2x+4= −3x−1 ⇒ x=−1 i y= 2 to S=(−1,2)
P=(4,2)
r =|SP|= 5
o : (x+1)2+(y−2)2=25
=================
Piszemy równanie dwusiecznej kąta wewnętrznego:
d1 : |3x−4y+36|=5|x−4| ⇒ 3x−4y+36= −5x+20 ⇒ y=2x+4
d2 : |4x+3y+23|=5|x−4| ⇒ 4x+3y+23= −5x+20 ⇒ y= −3x−1
S= d1∩d2 : 2x+4= −3x−1 ⇒ x=−1 i y= 2 to S=(−1,2)
P=(4,2)
r =|SP|= 5
o : (x+1)2+(y−2)2=25
=================
 1)
Wykorzystuję prostopadłość prostych:
a: 3x−4y+36=0
b: 4x+3y+23=0
k⊥m, n⊥OX
2) Obliczenia u Janka
C=(−8,3) , B=(4,12),A=(4,−13)
|AC|=20, |BC|=15, |AB|=20
3)
a+b=2r+2R
15+20=2r+25
r=5, r⊥n w punkcie styczności
S leży na prostej x=−1
4) Kreślę prostą równoległą do AC ( b) odległą od niej o 5.
CB→[12, 9] |CB|=15
1)
Wykorzystuję prostopadłość prostych:
a: 3x−4y+36=0
b: 4x+3y+23=0
k⊥m, n⊥OX
2) Obliczenia u Janka
C=(−8,3) , B=(4,12),A=(4,−13)
|AC|=20, |BC|=15, |AB|=20
3)
a+b=2r+2R
15+20=2r+25
r=5, r⊥n w punkcie styczności
S leży na prostej x=−1
4) Kreślę prostą równoległą do AC ( b) odległą od niej o 5.
CB→[12, 9] |CB|=15



 Jak wyżej C(−8,3) r=|CD|=|DO|=5
i z wektorów CD ⊥pr.CB to
→
CD= [3,−4] ⇒ D=(−8+3,3−4)= (−5,−1)
DO= [4,3] ⇒ O=(−5+4, −1+3) = (−1,2)
o: (x+1)2+(y−2)2=25
Jak wyżej C(−8,3) r=|CD|=|DO|=5
i z wektorów CD ⊥pr.CB to
→
CD= [3,−4] ⇒ D=(−8+3,3−4)= (−5,−1)
DO= [4,3] ⇒ O=(−5+4, −1+3) = (−1,2)
o: (x+1)2+(y−2)2=25

 Narysowałam proste zawierające boki trójkąta
i wybrałam równania tych dwusiecznych, które przecinają się
we wenętrzu trójkąta
i po ptokach
Narysowałam proste zawierające boki trójkąta
i wybrałam równania tych dwusiecznych, które przecinają się
we wenętrzu trójkąta
i po ptokach  Gdybyś uczył w szkole takimi "rozwlekłymi" metodami
to lekcja musiałaby trwać co najmniej 180 min
Pozdrawiam
Gdybyś uczył w szkole takimi "rozwlekłymi" metodami
to lekcja musiałaby trwać co najmniej 180 min
Pozdrawiam 
 ?
?

 " bo jeszcze pomyśli, że to ja mu tu wypominam, ale słusznie mnie również to nie
interesuje
" bo jeszcze pomyśli, że to ja mu tu wypominam, ale słusznie mnie również to nie
interesuje 

 Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
A=(x1,y1), B=(x2,y2), C=(x3,y3}
I=(xs,ys)
1) Współrzędne punktu D=(d1,d2).
Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
A=(x1,y1), B=(x2,y2), C=(x3,y3}
I=(xs,ys)
1) Współrzędne punktu D=(d1,d2).
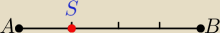 Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
Wiadomości:
1)
Podział odcinka AB w danym stosunku:
A =(x1, y1)
B=(x2, y2)
liczba k>0 (dodatnia),
Współrzędne środka okręgu wpisanego w trójkąt o danych wierzchołkach.
Wiadomości:
1)
Podział odcinka AB w danym stosunku:
A =(x1, y1)
B=(x2, y2)
liczba k>0 (dodatnia),
 2)
a)
2)
a)
 Dobranoc.
Dobranoc.




 Wybaczam.
Wybaczam.

 1)
W ΔABC: Z tw. o dwusiecznej kąta A
1)
W ΔABC: Z tw. o dwusiecznej kąta A

 Wszystko jasne dzięki <3
Wszystko jasne dzięki <3
 co Ty na to?
co Ty na to?
