Geometria mocno analityczna maja: Punkty A(−4,−5), B(0,−2) i C(2,1) tworzą trójkąt ABC. a) Wyznacz współrzędne trójkąta A'B'C', będącego obrazem trójkąta ABC w przekształceniu, w którym punkt A' jest obrazem punktu A w symetrii osiowej względem prostej y=−2, punkt B' jest obrazem punktu B w translacji o wektor [3,4], natomiast C' jest obrazem punktu C w

	1
jednokładności o środku w punkcie A i skali k=		.
	2

b) Oblicz o ile procent pole trójkąta ABC jest mniejsze od pola trójkąta A'B'C' Pomocy!

wredulus_pospolitus: No dobrze ... jak daleko sama zaszłaś z tym zadaniem

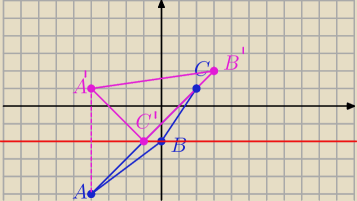
janek191: a) y = − 2 A' = ( − 4, 1) bo x' = x = −4 y ' = y + 2*3 = − 5 + 6 = 1 B =( 0, − 2) B' = ( 0 +3, −2 + 4) = ( 3, 2) C = ( 2, 1)

	1
k =
	2

	−4 + 2		−5 + 1
C ' = (		,		) = ( −1, −2)
	2		2

janek191: Pole Δ_ABC = P → AB = [ 0 − (−4), −2 −(−5)] = [ 4, 3] → AC = [ 2 −(−4), 1 − (−5)] = [ 6, 6 ] → → P = 0,5 * I det ( AB, AC ) I = 0,5*I 4*6 − 6*3 I = 0,5* I 6 I = 0,5*6 = 3 Pole Δ_A'B'C' można obliczyć analogicznie.