pole równoległoboku BKML w równoległoboku ABCD anonim2.0: W równoległoboku ABCD kąt przy wierzchołku A ma miarę 60stopni, punkt K jest środkiem boku BC, punkt L został wybrany na boku AB tak, że AL:LB = 1:2, a proste DK i CL przecinają się w punkcie M. Oblicz, jaką częścią pola równoległoboku ABCD stanowi pole czworokąta BKML.

kotek:

	29
PBKLM=		PABCD
	48

kotek:

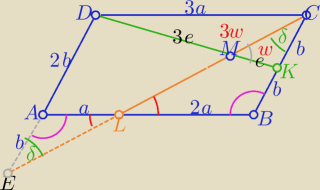
kotek: ΔBCL ∼ΔAEL z cechy (kkk) w skali k=2 ΔDEM∼ΔKCM w skali s=3 to P_CKM=w i P_DCM=3w zatem P_ABCD= 16w

	2		32		32		29
PBCL=		PABCD ⇒ PBCL=		w to PBKML=		w−w=		w
	3		3		3		3

zatem

	PBKML		29
		=
	PABCD		48

===========

anonim2.0: mam jeszcze dwa pytanka 1. Skąd wzięłaś/wziąłeś, że ²₃ P ABCD to ³²₃ w? 2. Jak obliczyłaś/obliczyłeś P ABCD =48?

kotek:

	1
PDCK=4w =		PABCD to PABCD=16w
	4

	2		32
PBCL=		*16w=		w
	3		3

	32		29
PBKLM=		w−w=		w
	3		3

PBKLM		29   w 3		29
	=		=
PABCD		16w		48

Jasne ?

anonim2.0: już tak, dziękuje

Leadeer: Obawiam się że wyżej jest pomyłka obliczeniowa:

	1
PABC =		*PABCD = 8w
	2

	2		2		1		2		16
PBCL =		*PABC =		*		*PABCD =		*8w =		w
	3		3		2		3		3

	16		13
stąd: PBKML = PLBC − PCMK =		w − w =		w
	3		3

	PBKML		13   w 3		13
czyli ostateczny stosunek:		=		=
	PABCD		16w		48

wredulus_pospolitus: zadanie z wczoraj: https://matematykaszkolna.pl/forum/421134.html informacja o kącie była zbyteczna

Mila: P− pole równoległoboku U kotka , pomyłka, 12: 22

	1
[BCL]=		P
	3

Sposób ładny.