Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne, w których suma promien xyz: Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne, w których suma promienia okręgu opisanego na podstawie i długości krawędzi bocznej jest równa d. Wyznacz długość krawędzi podstawy tego z rozpatrywanych ostrosłupów, który ma największą objętość. Oblicz tę objętość. czy mógłby ktoś samą dziedzinę wyznaczyć i wytłumaczyć, dlaczego od (0,1/2d)

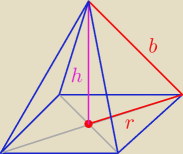
janek191: r + b = d Aby istniał ostrosłup musi być r < b, czyli r < 0,5 d

janek191: P_p = 0,5 *(2 r)² = 2 r² b = d − r więc h² + r² = b² = ( d − r)² = d² − 2 d r + r² h² = d² −2 d r h = √d² − 2 d r ⇒ d² −2 d r > 0 ⇒ d > 2 r ⇒ r < 0,5 d

	1		1
V =		Pp*h =		*2 r2*√d2 − 2 d r
	3		3