Trygonometria - wzory podwojonego kąta Alaias: Jeszcze raz proszę o pomoc w zadaniu Oblicz cos36^ocos108^o. Znalazłam nawet wzór na cos3α, ale nic mądrego nie wyszło − kręcę się w kółko

Eta:

	1
= −
	4

Alaias: No, dobrze jest wynik, ale mam podać jak do niego doszłam − a nie doszłam:(

Eta: cos108^o= −sin18^o i mamy

	2cos18o
−sin18o*cos36o / *
	2cos18o

	−sin36o*cos36o		2
=		/*
	2cos18o		2

	−sin72o		−cos18o		1
=		=		= −
	4cos18o		4cos19o		4

Eta: W ostatnim mianowniku oczywiście ma być 4 cos18^o

Alaias: Ooo! mnożę przez 1! A to dobry chwyt ! Dzięki

Eta:

Mariusz:

	√5+1
cos36°=
	4

cos108° = −cos72° cos72° = cos²36°−sin²36° cos72° = cos²36° − (1 − cos²36°) cos72° = 2cos²36° − 1

√5+1		(√5+1)2
	(1−		)
4		8

√5+1		5+1+2√5
	(1−		)
4		8

√5+1		6+2√5
	(1−		)
4		8

√5+1		3+√5
	(1−		)
4		4

√5+1		1−√5
	(		)
4		4

1−5
16

−4
16

	1
−
	4

Jeżeli nie masz do dyspozycji tablic to wartość cos36° dostaniesz z równania cos(5x)=−1 cos(x+y)=cos(x)cos(y)−sin(x)sin(y) cos(2x)=cos(x+x)=cos(x)cos(x)−sin(x)sin(x) cos(2x)=cos²(x)−sin²(x) cos(2x)=cos²(x)−(1−cos²(x)) cos(2x)=2cos²(x) − 1 sin(x+y)=sin(x)cos(y)+sin(y)cos(x) sin(2x)=sin(x+x)=sin(x)cos(x)+sin(x)cos(x) sin(2x)=2sin(x)cos(x) cos(4x)=cos(2*2x)=2cos²(2x)−1 cos(4x)=2(2cos²(x) − 1)²−1 cos(4x)=2(4cos⁴(x)−4cos²(x)+1)−1 cos(4x)=8cos⁴(x)−8cos²(x)+1 sin(4x)=sin(2*2x)=2sin(2x)cos(2x) sin(4x)=2(2sin(x)cos(x))(2cos²(x)−1) sin(4x)=8sin(x)cos³(x)−4sin(x)cos(x) cos(5x)=cos(x+4x)=cos(x)(8cos⁴(x)−8cos²(x)+1)−sin(x)(8sin(x)cos³(x)−4sin(x)cos(x)) cos(5x)=8cos⁵(x)−8cos³(x)+cos(x) − (8sin²(x)cos³(x)−4sin²(x)cos(x)) cos(5x)=8cos⁵(x)−8cos³(x)+cos(x) −sin²(x)(8cos³(x)−4cos(x)) cos(5x)=8cos⁵(x)−8cos³(x)+cos(x) −(1−cos²(x))(8cos³(x)−4cos(x)) cos(5x)=8cos⁵(x)−8cos³(x)+cos(x)−(8cos³(x)−4cos(x)−8cos⁵(x)+4cos³(x)) cos(5x)=8cos⁵(x)−8cos³(x)+cos(x)−(−8cos⁵(x)+12cos³(x)−4cos(x)) cos(5x)=16cos⁵(x)−20cos³(x)+5cos(x) Mamy zatem równanie 16cos⁵(x)−20cos³(x)+5cos(x)=−1 16cos⁵(x)−20cos³(x)+5cos(x)+1=0 Co po podstawieniu t=cos(x) daje równanie wielomianowe 16t⁵−20t³+5t+1=0 Można sprawdzić czy to równanie nie ma pierwiastków wielokrotnych licząc NWD(W(t),W'(t)) NWD(16t⁵−20t³+5t+1,80t⁴−60t²+5) 1/5t 16t⁵−20t³+5t+1:80t⁴−60t²+5 −(16t⁵−12t³+t) −8t³+4t+1 10t 80t⁴ − 60t² + 5:8t³−4t−1 −(80t⁴ − 40t² −10t) −20t²+10t+5 2t + 1 8t³−4t−1 : 4t²−2t−1 −(8t³−4t²−2t) 4t²−2t−1 −(4t²−2t−1) 0 NWD(16t⁵−20t³+5t+1,80t⁴−60t²+5)=4t²−2t−1 4t³+2t²−3t−1 16t⁵−20t³+5t+1:4t²−2t−1 −(16t⁵−8t⁴−4t³) 8t⁴−16t³+5t+1 −(8t⁴−4t³−2t²) −12t³+2t²+5t+1 −(−12t³+6t²+3t) −4t²+2t+1 −(−4t²+2t+1) 0 16t⁵−20t³+5t+1=(4t³+2t²−3t−1)(4t²−2t−1) 4t³+2t²−3t−1=4t³+4t²−2t²−3t−1 4t³+2t²−3t−1=4t²(t+1)−2t²−2t−t−1 4t³+2t²−3t−1=4t²(t+1)−2t(t+1)−1(t+1) 4t³+2t²−3t−1=(t+1)(4t²−2t−1) Zatem wielomian 4t³+2t²−3t−1 rozkłada się na (t+1)(4t²−2t−1)² t=−1 , odpada bo cos36° jest dodatni 4t²−2t−1=0

	2−√4+4*4
t1=
	2*4

	2+√4+4*4
t2=
	2*4

	2−√20
t1=
	8

	2+√20
t2=
	8

	2−2√5
t1=
	8

	2+2√5
t2=
	8

	1−√5
t1=
	4

	1+√5
t2=
	4

t₁ < 0 , więc odpada

	1+√5
Zostaje nam t2=
	4

i to jest wartość cos36°

Alaias: Niezła jazda

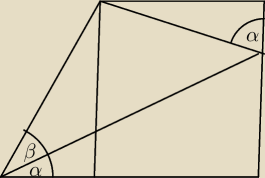
Mariusz: Gdybyś chciała jeszcze pokazać skąd się wziął wzorek na cosinus oraz sinus sumy to proponowałbym pobawić się geometrią Narysuj trójkąt prostokątny którego jednym z kątów jest kąt α Na ramieniu kąta α zbuduj kolejny trójkąt prostokątny którego jednym z kątów jest kąt β Jeżeli wierzchołek tego drugiego trójkąta zrzutujesz na ramię kąta α (ale nie na te które jest wspólne z kątem β) to dostaniesz trzy trójkąty i z nich trzeba będzie coś wywnioskować W tym trapezie masz cztery trójkąty prostokątne (choć rysunek tego nie oddaje) i powinnaś z tego wywnioskować wzorek na cosinusa i sinusa sumy

Mariusz: Wartości dla funkcji trygonometrycznych kąta α proponuję wziąć z tego trójkąta u góry Tak na dobrą sprawę ten sposób ma pewne ograniczenia więc chyba lepiej będzie poszukać jakiegoś ogólnego sposobu bo tutaj kąt o mierze α+β musi być kątem ostrym

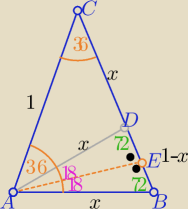
Eta: Z tw. o dwusiecznej (AD)

	x		1−x
		=		⇒ x2+x−1 =0 i x ∊(0,1)
	1		x

	√5−1
Δ=5 , √Δ= √5 x=
	2

W ΔABE :

	1−x		1		1		1		2		√5−1
sin18o =		=		(		−1)=		(		−1)= ...=
	2x		2		x		2		√5−1		4

	√5−1
sin18o=
	4

===================

	(√5−1)2		√5+1
cos36o=1−2sin218o = 1−		=.... =
	8		4

	√5+1
cos36o=
	4

===============

ite: Rozwiązanie z 14:37 jest najbardziej zgodne ze standardami nowej matury, gdzie wysoko będzie punktowana długość wypowiedzi (w celu ujednolicenia wymagań z wszystkich trzech przedmiotów obowiązkowych).

Kacper: Mariusz podziwiam Ja nawet bym tak długiej wiadomości nie dał rady wpisać