Pochodna krystiano:

	x+1
Wyznacz najmniejszą i największą wartość funkcji f(x) = f(x)=
	x2+3

w przedziale < −4;0 >.

Mila: 1)

	x+1
limx→±∞		=0
	x2+3

	1
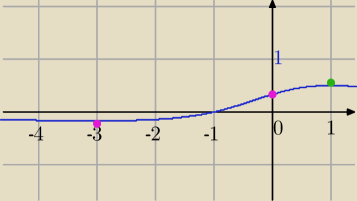
f(0)=		− największa wartość f(x)− bez pochodnej,
	3

2) Wartość najmniejsza:

	1*(x2+3)−(x+1)*2x
f'(x)=
	(x2+3)2

f'(x)=0⇔ −x²−2x+3=0⇔x=1∉<−4 ,0> lub x=−3 Rozpisz kiedy f'(x)>0 i ustal odpowiednie ekstrema

	1
f(−3)=−		− minimum w przedziale <−4,0>
	6

	−4+1		−3
f(−4)=		=
	16+3		19

	3		18		19		−1
−		=−		>−		=
	19		114		114		6

Ustal odpowiedź