Poproszę o rozwiązanie. Bartek: 1)Środkowe AD i A1D1 poprowadzone odpowiednio w trójkątach ABC i A1B1C1 mają równe długości. Wykaż, że jeśli |AB|=|A1B1| oraz |BC|=|B1C1|, to |AC|=|A1C1|. 2)Uzasadnij, że dla każdej liczby całkowitej n liczba: n(n⁴−1) jest podzielna przez 12. 3)Wykaż, że dla dowolnych liczb rzeczywistych a, b takich, że ab<0 jest prawdziwa równość a/b+b/a≥2. 4)Środkowe AD i A1D1 poprowadzone odpowiednio w trójkątach ABC i A1B1C1 mają równe długości. ∢CAD=∢C1A1D1 oraz ∢ADB=∢A1D1B1, to |AB|=|A1B1|.

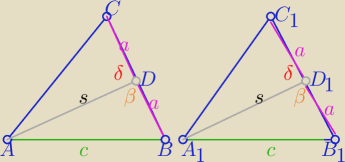
Eta: 1/ z cechy (bbb) ΔABD ≡ΔA1B1D1 to |∡ADB|=|∡A1D1B1|=β więc δ=180^o−β mają równe miary w obydwu trójkątach ADC i A1D1C1 to z cechy (bkb) ΔADC≡ΔA1D1C1 więc |AC|=|A1C1| c.n.w. zad3/ analogicznie ............... działaj zad2/ to nie jest prawdą bo dla n=2 2(2⁴−1)= 2*15=30 −− nie jest podzielne przez 12 może miało być : dla każdej n nieparzystej

Eta: zad 4/ analogicznie jak 1/ zad3/ (a−b)²≥0 a²+b²≥2ab / : ab>0

a		b
	+		≥2
b		a

c.n.w.

Eta senpai: A w zadaniu 2. przypadkiem nie miało być podzielne przez 30? Naturalnie najciężej jest udowodnic podzielność przez 5 (trzeba podstawić za "n" kolejno 5 liczb od n do n+4) Pozostałe dzielniki, tj. 3 i 2, uzyskamy łatwiutko po przekształceniu wyrażenia do najprostszej postaci: (n−1)*n*(n+1)*(n2+1) −−> iloczyn 3 kolejnych liczb naturalnych jest zawsze podzielny przez 3; iloczyn 2 kolejnych liczb naturalnych jest zawsze podzielny przez 2.