Znajdź styczne do paraboli przechodzące przez punkt Kacper: Znajdź styczne do wykresu funkcji f(x) = −x² − 9, które przechodzą przez punkt A = (4,0). Nie mam pojęcia od czego tu mogę zacząć

chichi: Ależ proszę bardzo https://matematykaszkolna.pl/strona/379.html

Kacper: Tylko że punkt A nie należy do wykresu funkcji

chichi: No to sam sobie odpowiedziałeś na pytanie

chichi: Skąd jest to polecenie?

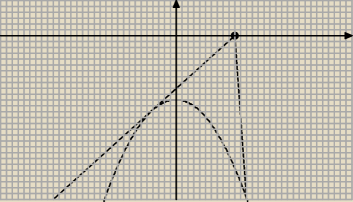
Kacper: Z rysunku wynika, że będą dwie styczne mam wyznaczyć ich wzory, nadal nie rozumiem w jaki sposób mogę to zrobić. Zadanie jest z matury próbnej układanej przez nauczycielkę.

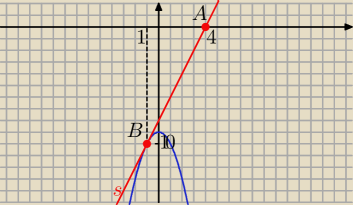
kotek: B=(−1,−10) s: y= 2x−8 ==========

kotek: Jest tylko jedna styczna !

Kacper: jak do tego doszedłeś?

kotek: s: y=a(x−4) s: y=ax−4a −x²−9=ax−4a x²−ax+4a−9=0 Δ =0 ................. i licz dalej....

chichi: f(x) = −x² − 9, k: y = ax + b ∧ A ∊ k ⇒ 0 = 4a + b ⇔ b = −4a, zatem y = ax − 4a −x² − 9 = ax − 4a ⇔ x² + ax − 4a + 9 = 0, 1 rozw. wtw. gdy Δ = 0: a² − 4(9 − 4a) = 0 ⇔ a² + 16a − 36 = 0 ⇔ (a + 18)(a − 2) = 0 ⇔ a ∊ {−18, 2} k₁: y = −18x + 72 ∨ k₂: y = 2x − 8

chichi: @kotek są dwie takie styczne

Kacper: Dzięki, już wszystko rozumiem.

kotek: Taaaaaaaaaaaaaaaaaaaaaaaaaak

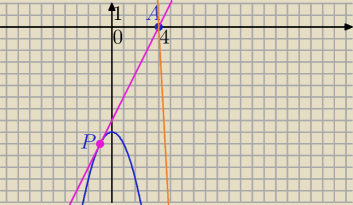
Mila: f(x) = −x² − 9 1) s: y=ax+b A = (4,0)∊s⇔0=4a+b, b=−4a s: y=ax−4a 2) równanie: −x²−9=ax−4a ma jedno rozwiązanie⇔Δ=0 x²+ax+9−4a=0 Δ=a²−4*(9−4a)=0 a²+16a−36=0 a=2 lub a=−18 s₁: y=2x−8 lub s₂: y=−18x+72 Możesz znaleźć punkty styczności: P=(−1,−10), Q=(.,.)

Min. Edukacji: Mila on już wszystko zrozumial😁 I co najważniejsze doszedl do tego sam wiec może zapamięta Gotowce zwykle wyrzuca sie do kosza i szybko zapomina.

==: Mila jak to Mila musi pisać po swojemu

Mila: No i co? Zaczęłam pisać, to widziałam tylko wpis 19:49.