dowód geometria Piotr: Pewien czworokąt ma następujące własności: − dwa naprzeciwległe boki są sobie równe i równe 2x − pozostałe dwa maja długość x i 3x. Ponadto wiemy, że na tym czworokącie opisano okrąg. Należy wykazać, ze to jest trapez.

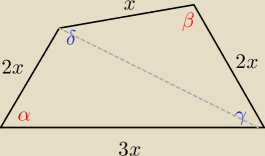
wredulus_pospolitus: skoro na czworokącie opisano okrąg, to znaczy, że suma przeciwległych kątów jest równa 180^o. Wiedząc to i stosując dwa razy tw. cosinusów, mamy: (2x)² + (3x)² − 12x²*cosα = (2x)² + (x)² − 4x²*cos(180−α) 8x² = 16x²*cosα −−−> cosα = 1/2 −−−> α = 60^o analogicznie (2x)² + (3x)² − 12x²*cosγ = (2x)² + (x)² − 4x²*cos(180−γ) 8x² = 16x²*cosγ −−−> cosγ = 1/2 −−−> γ = 60^o α = γ −−−> β = δ mamy trapez c.n.w.

Piotr: o, proste dziekuje