Pomoc z dwoma zadaniami [planimetria]
Maciek: Witam,
Prosiłbym o pomoc w rozwiązaniu dwóch zadań, które nie dają mi spokoju.
1. Na trójkącie równoramiennym o ramieniu √18 opisano okrąg o promieniu 3. Oblicz długość
podstawy tego trójkąta.
Próbowałem korzystać z:
− twierdzenia cosinusów,
− wzoru na R aby wyliczyć miarę jednego z kątów i wyszło 45 stopni,
− układu równań − twierdzenie Pitagorasa z dwóch trójkątów. Długość jednego z boków
'dodatkowego' trójkąta wyniosła zero.
Zazwyczaj jest dana podstawa w takich zadaniach i wówczas z obliczeniem czegokolwiek nie ma
problemu.
2. Oblicz pole trójkąta ABC, gdy |AB|=2, |BC|=2√3, kąt ACB=30 stopni.
Korzystałem z twierdzenia cosinusów, doprowadziłem do równania kwadratowego, z którego wyszła
'normalna' delta ale długość trzeciego boku wyniosła 2 lub 4.
Z góry dzięki!
21 mar 01:09
wredulus_pospolitus:
(1) to pokaż jak próbowałeś
PS. skoro wyszło Ci, że jeden z kątów (przy podstawie) wynosi 45o to już jest de facto koniec
zadania −−− stąd znasz kąty ... widzisz jaki to trójkąt ... wiesz ile wynosi podstawa
21 mar 09:56
wredulus_pospolitus:
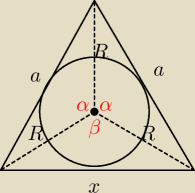
(1) metoda 1
z tw. cosinusów:
a
2 = R
2 + R
2 − 2R
2*cosα , podstawiamy:
(
√18)
2 = 3
2 + 3
2 − 2*3
2*cosα
18 = 18 − 18cosα
18cosα = 0 −−−> α = 90
o
stąd: β = 360
o − 2*α = 180
o
ergo ... środek okręgu leży na podstawie (w połowie podstawy) ... więc mamy trójkąt prostokątny
... podstawa równa 2R = 6
21 mar 10:05
wredulus_pospolitus:
(1) metoda 2
| | a | | √2 | |
R = |
| −−−> sinγ = |
| −−−> γ = 45o |
| | sinγ | | 2 | |
kąt przy podstawie wynosi 45
o −−−> kąt przy wierzchołku = 90
o (mamy trójkąt prostokątny)
x = 2R = 6
21 mar 15:13
wredulus_pospolitus:
(1) metoda 3
| | x | |
R = |
| ; x2 = a2 + a2 − 2a2*cosγ |
| | 2sinγ | |
x = 2Rsinγ ; x
2 = 2a
2(1 − cosγ)
4R
2sin
2γ = 2a
2(1−cosγ)
| | 1 | |
1 = |
| −−−> 1 + cosγ = 1 −−−> cosγ = 0 −−−> γ = 90o |
| | 1+cosγ | |
kąt przy wierzchołku kątem prostym, trójkąt prostokątny −−−> x = 2R = 6
21 mar 15:17
wredulus_pospolitus:
Ostatnia metoda niepotrzebnie 'trudna' w porównaniu z poprzednimi
21 mar 15:18
Mila:
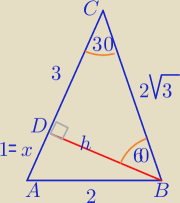
I ) ΔABC−
1)ΔCDB− Δekierkowy :90
o, 60
o,30
o
h=
√3
|DC|=3
2) W ΔADB:
x
2+h
2=2
2⇔x
2+3=4
x=1
|AC|=4
3)
W drugim przypadku masz Δrozwartokątny równoramienny o kącie 120
o między ramionami o dł. 2.
21 mar 21:46
 (1) metoda 1
z tw. cosinusów:
a2 = R2 + R2 − 2R2*cosα , podstawiamy:
(√18)2 = 32 + 32 − 2*32*cosα
18 = 18 − 18cosα
18cosα = 0 −−−> α = 90o
stąd: β = 360o − 2*α = 180o
ergo ... środek okręgu leży na podstawie (w połowie podstawy) ... więc mamy trójkąt prostokątny
... podstawa równa 2R = 6
(1) metoda 1
z tw. cosinusów:
a2 = R2 + R2 − 2R2*cosα , podstawiamy:
(√18)2 = 32 + 32 − 2*32*cosα
18 = 18 − 18cosα
18cosα = 0 −−−> α = 90o
stąd: β = 360o − 2*α = 180o
ergo ... środek okręgu leży na podstawie (w połowie podstawy) ... więc mamy trójkąt prostokątny
... podstawa równa 2R = 6
 I ) ΔABC−
1)ΔCDB− Δekierkowy :90o, 60o,30o
h=√3
|DC|=3
2) W ΔADB:
x2+h2=22⇔x2+3=4
x=1
|AC|=4
3)
I ) ΔABC−
1)ΔCDB− Δekierkowy :90o, 60o,30o
h=√3
|DC|=3
2) W ΔADB:
x2+h2=22⇔x2+3=4
x=1
|AC|=4
3)