nierówności człowiekniewiadomo: Hej, pomoże ktoś Zad 1: Rozwiąż nierówność √(x + 7) − 5 ≤ − |x|

I'm back: Jakbyśmy chociaż wiedzieli gdzie ten pierwiastek się konczy

człowiekniewiadomo: x + 7 jest pod pierwiastkiem

janek191: √x + 7 − 5 ≤ − I x I √x + 7 ≤ 5 − I x I x + 7 ≥ 0 ⇒ x ≥ − 7 Rozwiąż w przedziałach.

stachu: 1: x∊ (−∞, 0) √x+ 7 ≤ 5+x | ()² x + 7 ≤ x² + 10x + 25 0 ≤ x² + 9x + 18 x1 = −3 x2 = −6 2: x∊ (0, ∞) √x+ 7 ≤ 5 − x | ()² x + 7 ≤ x² − 10x + 25 0 ≤ x² − 11x + 18 x1 = 9 x2 = 2 O to chodziło ?

Mila: √x+7−5≤−|x| D_r=<−7,∞) √x+7≤5−|x| Lewa strona nierówności jest nieujemna Zatem dla 5−|x|<0 nierówność nie jest spełniona |x|>5⇔ x<−5 lub x>5 wyłączamy z dziedziny równania 1) x∊<−5,0) Mamy równanie: |x|=−x √x+7≤5+x /² obie strony są nieujemne x+7≤(5+x)²⇔ (Rozwiąż ) −3≤x<0 lub x∊<0,5> Wtedy mamy nierówność: p{x+7)≤5−x obie strony nieujemne x+7≤(5−x)²⇔ (Rozwiąż) 0≤x≤2 Odp: x∊<3,2>

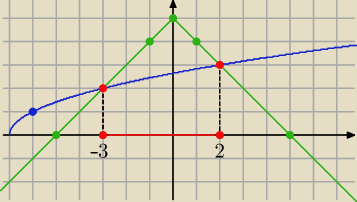
Eta: graficznie: f(x)=√x+7 g(x)= −|x|+5 Odp: x∊ <−3,2> =========