Sinus i cosinus kąta
monia85: Znajdź sin i cos kąta QPR jeśli;
P= (−1,−3),Q= (1,1),R= (3,5)
16 mar 21:19
wredulus_pospolitus:
1) wyznacz długości boków trójkąta QPR
2) skorzystaj z tw. cosinusów w celu wyznaczenia cosinusa pożądanego kąta
3) skorzystaj z jedynki trygonometrycznej w celu wyznaczenia sinusa tegoż kąta
kooooniecccc
16 mar 21:52
chichi:
| | [4,8] ∘ [2,4] | | 40 | |
Niech: |∡QPR| = α, zatem: cos(α) = |
| = |
| = 1 |
| | √42 + 82√22 + 42 | | 40 | |
@
wredulus chcesz utworzyć trójkąt z punktów, które są współliniowe?
16 mar 22:12
janek191:
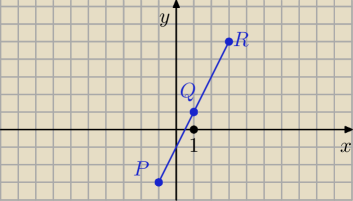
α = 0
o
sin α = 0
cos α =1
17 mar 09:11
TANG XIN: wredulus wcale nie musiał wiedziec że te punkty są wspóliniowe
Dlaczego ? ja zawsze mówie ze nalezy wykonać rysunek nawet jesli to jest najprostsze polecenie
.
Jednak odzywają sie glosy ze nie ma potrzeby a wrecz ze nie potrzeba .Tutaj mamy własnie taki
przyklad.
To co napisał wredulus jet według mnie przwidłowe bo z obliczen wyjdzie ze tak wlasnie jest
17 mar 09:31
chichi:
No to jesteś w błędzie
17 mar 11:23
chichi:
P. S. Widać gołym okiem, że są współliniowe, bez robienia jakiegokolwiek rysunku, przecież ja
nie załączyłem żadnego rysunku
17 mar 11:25
Eta:
A jak oko jest zasłonięte ciemnymi okularami ?
17 mar 13:18
chichi:
Jeszcze nie rozwiązywałem zadań w ciemnych okularach, muszę spróbować
17 mar 13:20
Eta:
17 mar 13:24
TANG XIN:
chichi a jak ktoś nie jest tak bystry jak Ty i
kotek?(w pozytywnym tego słowa
znaczeniu)
Owszem nie załaczyłeś ale mogłes go miec zrobiony przed sobą
17 mar 15:28
chichi:
A jak ktoś nie potrafi rozwiązywać równań kwadratowych to co?
17 mar 15:32
chichi:
Nie miałem rysunku, spojrzałem na współrzędne punktów zobacz na 'x' wzrasta o 2 jednostki, a na
'y' o 4 − wniosek jest prosty. Sposób wredulusa i tak jest dłuższy więc robiłbym swoją metodą
nawet jeśli byłby to trójkąt
17 mar 15:34
TANG XIN:
Jak ktoś nie potrafi rozwiązywać równanń kwadratowych graficznie to polecam Zofia Krygowska
Konstrukcje geometryczne na płaszczyznie (stara bo 1958r)
17 mar 15:49
TANG XIN: Tutaj mozna policzyc z iloczynu skalarnego wektorów cos kata co zrobiłes
Natomiast sin kąta miedzy wektorami mozna obliczyć ze wzoru
| | d(u,v) | |
sin∡(u,v)= |
| |
| | |u|*|v| | |
d(u,v) to wyznacznik pary wektorów u i v
d(u,v)= a
1b
2−a
2b
1
u={a
1,b
1] v={a
2,b
2]
tam wszędzie nad u i v maja być strzałki bo to są wektory
TUtaj od razu z iloczynu skalarnego wyszlo 0 stopni wiec nie ma potrzeby liczyc sinusa kąta
ja to rozumiem .Zrobienie rysunku w niczym nie przeszkadza (według mnie ) . Odpoczywaj
17 mar 16:02
wredulus_pospolitus:
@chichi −−− nie przyglądałem się punktom −−− w momencie liczenia długości bym doszedł do tego
wniosku (nawet jeżeli bym nie zrobił rysunku).
17 mar 16:46
chichi:
Rzecz jasna. Chciałem tylko zwrócić uwagę, że nie jest to trójkąt
17 mar 16:51
Mila:
chichi jaki to język?
Triunghi si patrulater inscris in cerc si circumscrise cercului ...
17 mar 18:07
chichi:
Tłumacz mówi, że rumuński. Znam wielu rumunów − wspaniali geometrzy, oni ją kochają
17 mar 18:18
Mila:
chichi Dziękuję.
Pojawiły się materiały na youtube, nie wiem, czy to coś nowego. To materiały z geometrii.
Mam sentyment do Rumunów. Tato był ratowany , goszczony, jako żołnierz − uchodźca
pokonanej armii polskiej w kampanii wrześniowej w 1939 roku.
To wspaniały naród.
17 mar 18:57
Mariusz:
Pole z wyznacznika , sinus z wzoru na pole
Co do cosinusa tak , twierdzenie cosinusów
17 mar 19:03
Mariusz:
Chichi na upartego można, na wikipedii kiedyś nazwali to przypadkiem zdegenerowanym
Mimo to wzór na pole z wyznacznikiem działa także dla przypadku zdegenerowanego
17 mar 19:07
chichi:
To prawda, są bardzo sympatyczni
17 mar 19:16
Mariusz:
Kąty w tym trójkącie to 180° , 0° , 0° , pole wynosi zero
Chichi wracając do sposobu na równanie dwusiecznej
Mając dane wierzchołki trójkąta ABC
1. Piszemy równania prostych w których zawierają się ramiona kąta
2. Na jednym z ramion kąta obieramy sobie punkt D
3. Piszemy równanie okręgu o środku w punkcie A i promieniu AD
4. Punkt E to przecięcie okręgu z prostą zawierającą drugie ramię kąta
5. Piszemy równanie prostej przechodzącej przez punkty DE
6. Piszemy równanie prostej prostopadłej do prostej DE i przechodzącej przez punkt A
Tak na dobrą sprawę to kroki 5. i 6. można połączyć w jeden
Teraz problemem jest to że w kroku 4 piszemy układ równań (okrąg i prosta)
z czego wychodzą nam dwa punkty E ale tylko jeden daje dwusieczną kąta wewnętrznego
Chichi jaki warunek logiczny mi byś zaproponował ?
Najlepiej z uzasadnieniem jego poprawności
17 mar 19:32