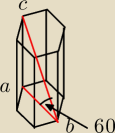
help me! szman03: W graniastosłupie prawidłowym sześciokątnym dłuższa przekątna ma długość 12 cm (odc. bc) i jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. Oblicz: a) Pole powierzchni tego graniastosłupa. b) Objętość tego graniastosłupa. c) Tangens kąta nachylenia krótszej przekątnej tego graniastosłupa do płaszczyzny podstawy.

wredulus_pospolitus: 1) z sin60^o masz wysokość graniastosłupa 2) z cos60^o masz dłuższą przekątną podstawy (sześciokąta foremnego), która jest równa 2a (gdzie a −−− bok sześciokąta foremnego) To Ci wystarczy aby zrobić podpunkty (a) i (b) 3) krótszą podstawę możesz wyliczyć z chociażby tw. cosinusów (pamiętaj że kąt wewnętrzny w sześciokącie foremnym jest równy 120^o ) Mając krótsza podstawę i wysokość graniastosłupa ... wyznaczasz podpunkt (c). Powodzenia

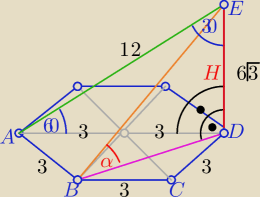kotek: W ΔADE "ekierkowym"o kątach ostrych 60^o,30^o : |AD|=6=2a ⇒ a=3 i H=6√3 P_c= 2P_p+6aH =..... V= P_p*H=.... w ΔBDE : |BD|=a√3= 3√3

	6√3
to tgα=
	3√3

tgα= 2