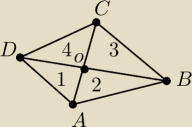
 Przekątne AC i BD czworokąta wypukłego ABCD dzielą go na 4 trójkąty o polach P1, P2,
, P3, P4.
Wykaż, że P1 * P3 = P2 * P4.
Na rysunku trójkąt nr. 1 to P1, trójkąt nr. 2 to P2, itd..
Przekątne AC i BD czworokąta wypukłego ABCD dzielą go na 4 trójkąty o polach P1, P2,
, P3, P4.
Wykaż, że P1 * P3 = P2 * P4.
Na rysunku trójkąt nr. 1 to P1, trójkąt nr. 2 to P2, itd..
| P4 | |DO| | ||
= | − Δ mają taką samą wysokość | ||
| P3 | |OB| |
| P1 | |DO| | ||
= | − j.w | ||
| P2 | |OB| |
| P4 | P1 | ||
= | ⇔ | ||
| P3 | P2 |
