trojkat szman03: Dane są punkty A = (−3, √3), B = (−7, √3). Wyznacz współrzędne punktu C należącego do osi OY, tak, aby pole trójkąta ABC było równe 12.

chichi: A = (−3, √3), B = (−7, √3), C = (0, y) vec(AB) = [−4, 0] ∧ vec(AC) = [3, y − √3]

	1		−4 0 3 y − √3
P =		|		| = |2√3 − 2y| = 12
	2

⇒ y = √3 − 6 ∨ y = √3 + 6, zatem: C₁ = (0, √3 − 6) ∨ C₂ = (0, √3 + 6)

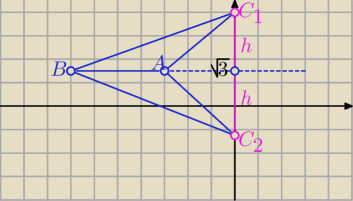
kotek: |AB|=4 P=2h=12 h=6 C₁(0,......) C₂=(0,........)

chichi: Super rozwiązanie