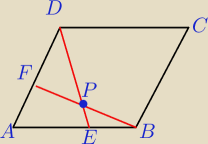
matura rozszerzona Marta: Kąt ostry rombu ABCD ma miarę 60 stopni . Na bokach AB i AD tego rombu wybrano punkty – odpowiednio – E i F takie, że |BE | = |AF | = 1/3|AB | . Odcinki BF i DE przecinają się w punkcie P (zobacz rysunek). Wykaż, że punkt P leży na okręgu opisanym na trójkącie BCD .

Marta: Na pewno wiem, że trójkąt BCD jest równoboczny, więc można na nim opisać okrąg, ale jak udowodnić, że punkt P leży na okręgu?

Marta: ?

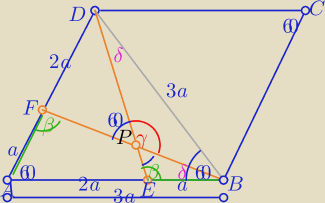
Eta: trójkąty ABF i BED są przystające z cechy (kbk) trójkatyBEP i BAF są podobne z cechy (kkk) to |∡BPE|=|∡BAF|= 60^o zatem kąt |∡BPD|=γ=180^o−60^o=120^o więc na czworokącie BCDP można opisać okrąg, który jest okręgiem opisanym także na ΔBCD więc P należy do tego okręgu co kończy dowód

Marta: Dziękuję

Eta: miało być ......... z cechy (bkb)