trójkąt mat-geo: Dany jest trójkąt prostokątny o przeciwprostokątnej długości c Dwusieczna kąta prostego zawarta w tym trójkącie ma długość d Wyznacz pole tego trójkąta

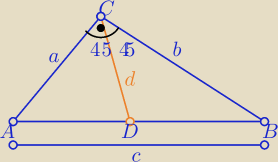
Eta: 2P=ab to 2ab=4P a²+b²=c² ⇒ (a+b)²−2ab=c²⇒ (a+b)²=c²+2ab ⇒ (a+b)²=c²+4P

	√2ab
d=		−− długość dwusiecznej (i obustronnie do kwadratu) / 2
	a+b

d²(a+b)²=2a²b² i a²b²=4P² d²(c²+4P)= 8P² 8P²−4d²P−d²c²=0 Δ=16d⁴+32d²c² , √Δ=4d√d²+2c²

	4d2+4d√d2+2c2
P=		, c>d
	16

	d2+d√d2+2c2
P=
	4

================

Mariusz: Eta nie każdy od razu zauważy skąd się ten wzorek na długość dwusiecznej wziął Tutaj mamy trójkąt prostokątny więc obliczenia się uproszczą ale w dowolnym trójkącie już by było trudniej wyprowadzić ten wzorek na długość tym bardziej gdybyśmy mieli takowy wyprowadzić w pamięci Tutaj aby wyprowadzić ten wzorek na długość dwusiecznej zastosowałem: twierdzenie sinusów, wzory redukcyjne , wzór na sinus sumy, Korzystając z tego że mamy trójkąt prostokątny zamieniłem wartości funkcyj trygonometrycznych na odpowiednie stosunki długości boków

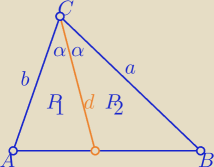
Eta: Dla trójkąta dowolnego :

	1		1
PABC=		ab*sin(2α) =		ab*2sinαcosα
	2		2

	1		1
P1=		bdsinα , P2=		adsinα
	2		2

to 2absinαcosα=bdsinα+adsinα \ : sinα≠0 2abcosα= d(a+b)

	2abcosα
d=
	a+b

===============

	√2
dla trójkąta prostokątnego α=45o , sinα=
	2

	√2ab
to d=
	a+b

============= i po ptokach

Eta:

	√2
cosα=
	2

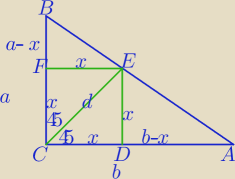
Mila: || sposób− jeśli uczeń nie zna wzoru na długość odcinka dwusiecznej.

	1
PΔABC=		a*b
	2

2P=a*b 1) 2x²=d²

	d2
x2=		− pole kwadratu ABCD
	2

	d
x=
	√2

2) a²+b²=c²⇔(a+b)²−2ab=c² (a+b)=√c²+4P 3)

	d2		1		1
P=		+		(a−x)*x+		(b−x)*x /*2
	2		2		2

2P=d²−2x²+(a+b)*x

	d
2P=(a+b)*x⇔2P=√c2+4P*
	√2

2√2P=d*√(c²+4P) /² 8P²=d²*c²+4Pd² 8P²−4d²P−c²*d²=0 ================ dalej jak u Ety, albo bez delty.