Okrąg wpisany i opisany na trapezie
Werve: Na trapezie można opisać okrąg i wpisać w niego okrąg. Oblicz r i R, jeśli przekątna równa się
10, a obwód wynosi 24.
9 mar 19:40
Werve: Wg moich obliczeń, to zadanie jest nie do obliczenia:
1) Ramiona mają po 6, a podstawy 12−x i x;
2) Używamy twierdzenia cosinusów:
102=x2+62+2*x*6*cosa
102=62+(12−x)2−2*6*(12−x)*cosa
3)Nie użyłem tu, jak dla mnie prostych przekształceń, których użyłem, bo dla mnie są jasne.
Czy popełniłem tu błąd?
9 mar 19:43
chichi:
No nie, ale masz jedno równanie z dwoma niewiadomymi więc znajdź jeszcze jedno równanie. Na
przykład napisz tw. Carnota (cosinusów) jeszcze raz, czyli spójrz na trójkąt po drugiej
stronie przekątnej do tego, do którego napisałeś
9 mar 19:49
Werve: Napisałem te równania dla dwóch stron
9 mar 19:51
Werve: Widać, że w jednej stronie jest + z cosinusem, a z drugiej −
9 mar 19:51
Werve: I też jakbyś mi to mógł po prostu policzyć to byłbym wdzięczny bo chce mieć pewność że w tych
danych jest błąd
9 mar 19:53
chichi:
Ale ja nie wiem czy szedłbym tą drogą, jak usiądę do komputera to odpisze
9 mar 20:07
Werve: Droga nie wiem najłatwiejsza, ale jeśli mój sposób jest dobry a wyjdzie sprzeczność to obaliłem
zadanie na kartkówce, więc się cieszę
9 mar 20:18
chichi:
Ale w jaki sposób Ty "obaliłeś to zadanie"
9 mar 20:31
Werve: że po prostu nie da się wyliczyć długości podstaw dla tych danych moim sposobem
9 mar 20:35
chichi:
Jeżeli pokazałeś, że ten układ nie ma rozwiązań to ok. Natomiast jeżeli go nie rozwiązałeś, bo
nie potrafiłeś, to to żadne obalenie
9 mar 20:41
Mila:
Czy dobrze obwód jest wpisany?
9 mar 20:43
Eta:
Przy takich danych ..... sprzeczność
9 mar 20:48
Mila:
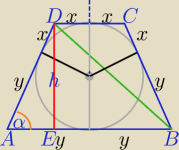
1) Trapez równoramienny
obw=4x+4y
4x+4y=24
x+y=6
3) W ΔDEB:
h=2r
|EB|=x+y
(2r)
2+(x+y)
2=10
2
4r
2+6
2=100
4r
2=64
r
2=16
r=4
4)
W ΔAED: h=8, |AD|=6 sprzeczność bo przeciwprostokątna jest dłuższa
od każdej z przyprostokątnych.
Oto co otrzymujemy dalej:
| | h | | 2r | | 8 | |
sinα= |
| = |
| = |
| >1 sprzeczność. |
| | x+y | | 6 | | 6 | |
Błędne dane.
9 mar 20:50
chichi:
Sprzeczność jest oczywista, pytanie czy autor ją wykazał, czy jest tak jak napisałem o
20:41
9 mar 20:51
Eta:
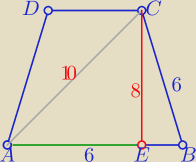
a+b=2c to a+b=12 i c=6
w ΔEBC : c<h −− sprzeczność
9 mar 20:53
chichi:
10
2 = x(12−x) + 6
2 ⇔ x
2 − 12x + 64 = 0 ⇔ (x − 6)
2 + 28 = 0 − sprzeczne!
9 mar 20:53
Eta:
Ma być: h=2r=8
9 mar 20:56