W ostrosłupie prawidłowym trójkątnym kąt nachylenia krawędzi bocznej do płaszczy Filip: W ostrosłupie prawidłowym trójkątnym kąt nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy 60°, a krawędź podstawy ma długość 4. Oblicz pole powierzchni bocznej i objętość tego ostrosłupa.

wredulus_pospolitus: 1) rysunek 2) wyznaczasz wysokość podstawy 3) zauważasz gdzie 'spada' wierzchołek ostrosłupa 4) z funkcji trygonometrycznej wyznaczasz wysokość ostrosłupa 5) obliczasz objętość 6) z funkcji trygonometrycznej wyznaczasz długość krawędzi bocznej 7) obliczasz wysokość ściany bocznej (np. tw. Pitagorasa) 8) obliczasz pole powierzchni bocznej Kooooniec

Filip: Wyszło mi, że Ppb = 4√39 a V = ^16√3₃. Chciałbyś sprawdzić czy mam dobrze?

wredulus_pospolitus: pokaż obliczenia

Filip: To wziąłem wycinek trójkąta, 90°, 60° i 30°. Podstawa to ²₃h a h to ^a√3₂ a = 4. Stąd podstawa ^4√3₃. To z funkcji mi wyszło, że H, wysokość ostrosłupa to 4. I objętość to ¹₃ * Pp * H. Pp to ^a2√3₄. Więc objętość mi wyszła ^16√3₃. Następnie wziąłem kolejny wycinek trójkąta, krawędź boczna, połowa podstawy i wysokość ściany bocznej. Z tw. Pitagorasa mi wyszło, że wysokość ma ^2√39₃. No i na koniec pole boczne obliczyłem to 3 * ¹₂ * a * h.

Filip: Przy pierwszym wycinku trójkąta, obliczyłem również krawędź boczną to wyszło mi ^8√3₃

I'm back: Jest ok

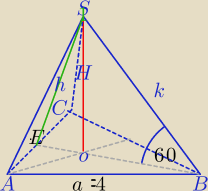
Mila: 1) W ΔABC: P_ΔABC=4√3 |EB|=2√3

	2√3		4√3
|EO|=		, |OB|=
	3		3

2) W ΔSOB:

	4√3
H=		*√3=4
	3

	1		16√3
3) V=		*4√3*4=
	3		3

==================== 3) W ΔSOE: h²=H²+|EO|²

	4		52
h2=16+		=
	3		3

	2√13		2√39
h=		=
	√3		3

	1		2√39
Pb=3*		*4*		⇔
	2		3

P_b=4√39 ======