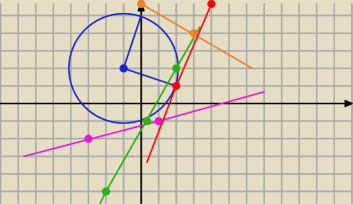
równanie okręgu Axelek2117: Zadanie 3. Okrąg o środku w punkcie O(−1,2) i promieniu pierwiastek z 10 ma dwa punkty wspólne z prostą AB, gdy: A. A(−3,−2) B(1,−1) B. A(−2,−5) B(2,2) C A(0,5) B(3,4) D. A(2,1) B(4,7)

Tadeusz: masz dwa punkty A i B ... znasz więc równanie prostej przechodzącej przez te punkty. Policz odległość środka okręgu od prostej i wnioskuj

Eta: A , B , C, D Odp: B

janek191:

	−1 − (−2)		1
a =		=
	1 − (−3)		4

	1
y =		x + b
	4

	1		5
−1 =		*1 + b ⇒ b = −
	4		4

	1		5
y =		x −		/ * 4
	4		4

x − 4 y − 5 = 0 Odległość tej prostej od O(−1,2)

	I 1*(−1) + (−4)*2 − 5I		14
d =		=		> r = √10
	√17		√17

Brak punktów wspólnych z okręgiem o środku O(−1,2) i r = √10