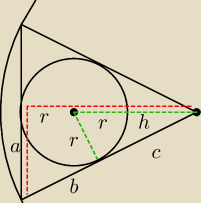
 1) przekątne prostokąta wpisanego w okrąg przecinają się w środku tegoż okręgu
2) trójką PBC to trójkąt równoboczny, związku z tym ABP to trójkąt równoramienny o ramieniu R i
kącie przy wierzchołku równym 120o.
b+c = R =
1) przekątne prostokąta wpisanego w okrąg przecinają się w środku tegoż okręgu
2) trójką PBC to trójkąt równoboczny, związku z tym ABP to trójkąt równoramienny o ramieniu R i
kącie przy wierzchołku równym 120o.
b+c = R = 
| a | √3 | √3 | ||||
sin60o = | = | −−−> a = | R | |||
| R | 2 | 2 |
| r | 15 | √3 | ||||
sin60o = | = | = | −−−> h = 10√3 − 15 | |||
| r+h | 15+h | 2 |
| 3 | ||
a2 + (r + (r+h))2 = R2 −−−> | R2 + (15 + 10√3 − 15)2 = R2 | |
| 4 |
 dziękuję! nie pomyślałam żeby rozbijać to w taki sposób
w tw. Pitagorasa jest mały błąd (r + (r+h)) daje 15 − 10√3
czyli
R = √2100−1200√3
P = (175−100√3)π
dziękuję! nie pomyślałam żeby rozbijać to w taki sposób
w tw. Pitagorasa jest mały błąd (r + (r+h)) daje 15 − 10√3
czyli
R = √2100−1200√3
P = (175−100√3)π
 Ale Ty też masz błąd 2r+h = 15+10√3
Ale Ty też masz błąd 2r+h = 15+10√3 
| R2 | R | |||
(15+10√3)2 = | −−−> 15 + 10√3 = | −−−> R = 30 + 20√3 | ||
| 4 | 2 |
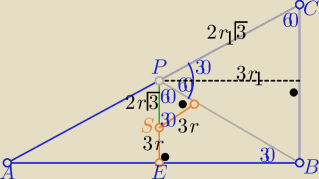 Można też tak z trójkątów "ekierkowych" o katach ostrych 30o,60o
wprowadzam dla łatwości obliczeń : 3r=15
r1−− długość promienia okręgu wpisanego w ΔBCP
|PE|=2r√3+3r = r(3+2√3) i |PB|=2|PE|= 2r1√3
to
2r1√3= 2r(3+2√3) / 2
12 r12=4r2(21+12√3) 3r=15 to r=5
r12=25(7+4√3)
Pole koła wpisanego w ΔBCP:
Pk =25(7+4√3)π
==============
Można też tak z trójkątów "ekierkowych" o katach ostrych 30o,60o
wprowadzam dla łatwości obliczeń : 3r=15
r1−− długość promienia okręgu wpisanego w ΔBCP
|PE|=2r√3+3r = r(3+2√3) i |PB|=2|PE|= 2r1√3
to
2r1√3= 2r(3+2√3) / 2
12 r12=4r2(21+12√3) 3r=15 to r=5
r12=25(7+4√3)
Pole koła wpisanego w ΔBCP:
Pk =25(7+4√3)π
==============
 bo właśnie coś mi się tu nie zgadzało
bo właśnie coś mi się tu nie zgadzało  z tymi własnościami kątów 90,60,30 też spoko ale żeby się nie pogubić w oznaczeniach
z tymi własnościami kątów 90,60,30 też spoko ale żeby się nie pogubić w oznaczeniach  R = √2100+1200√3
P = (175+100√3)π
R = √2100+1200√3
P = (175+100√3)π