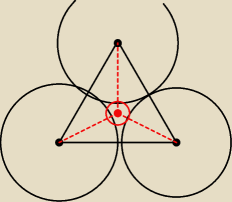
 robimy przekrój tychże kul i otrzymujemy taki oto rysunek.
Mamy trzy okręgi o promieniu r. Łącząc środki tychże okręgów otrzymujemy trójkąt równoboczny o
boku 2r.
wystarczy wyznaczyć x promień małego okręgu (np. z tw. cosinusów):
(2r)2 = (r+x)2 + (r+x)2 − 2(r+x)*2*cos(120o) −−−>
−−−> 4r2 = (r+x)2*(2+1) −−−> 3x2 + 6xr − r2 = 0
Δx = 36r2 + 12r2 = 24r2 −−−> √Δx = 2√6r
x1 = ....
x2 = ....
wybierasz x>0 i koniec zadania
robimy przekrój tychże kul i otrzymujemy taki oto rysunek.
Mamy trzy okręgi o promieniu r. Łącząc środki tychże okręgów otrzymujemy trójkąt równoboczny o
boku 2r.
wystarczy wyznaczyć x promień małego okręgu (np. z tw. cosinusów):
(2r)2 = (r+x)2 + (r+x)2 − 2(r+x)*2*cos(120o) −−−>
−−−> 4r2 = (r+x)2*(2+1) −−−> 3x2 + 6xr − r2 = 0
Δx = 36r2 + 12r2 = 24r2 −−−> √Δx = 2√6r
x1 = ....
x2 = ....
wybierasz x>0 i koniec zadania
| 2 | ||
Natomiast wiemy, że środek okręgu opisanego na trójkącie równobocznym ma promień R = | h = | |
| 3 |
| 2 | a√3 | 2r√3 | ||||
* | = | |||||
| 3 | 2 | 3 |
| 2√3r | 2√3 − 3 | |||
związku z tym: x = | − r = | r | ||
| 3 | 3 |