Kąty, półprosta Karolina: Wyznacz miary kątów AOB i BOC, wiedząc że, kąt AOB + kąt BOC=225 stopni i przedłużenie półprostej OA dzieli kąt BOC w stosunku 1:3. Rozpatrz dwa przypadki. Jest to zad. 7.8 OE zbiór zadań poziom podstawowy. Wiem, jak to zadanie należałoby rozwiązać wg autora, tylko chciałam zapytać, czy to zadanie: 1) po pierwsze jest dobrze sformułowane? Wydaje mi się, że nie można przedłużyć półprostej OA przez punkt O, bo to zaprzecza definicji półprostej. 2) gdyby założyć, że autor się pomylił i chciał napisać półprosta AO zamiast OA, to wydaje mi się, że wtedy nadal nie mielibyśmy możliwości przedłużenia, co wynika z definicji kąta, że zbudowany jest on z dwóch półprostych. 3) jeśli podany jest kąt BOC w stosunku 1:3 to również wydaje mi się, że przy podawaniu stosunku kolejność powinna zostać zawsze zachowana, więc jedynie kąt BOX =α oraz kąt XOC = 3α, co z kolei powinno wykluczyć istnienie dwóch przypadków. Z góry bardzo dziękuję za informację, co Państwo sądzą na temat moich wątpliwości, bo być może się mylę

chichi: Dwie półproste przedłużają się jeśli kąt między nimi wynosi 180^o, wówczas się łączą i tworzą prostą, wszystko jest jasne. Ty widocznie nie rozumiesz o co chodzi.

Karolina: Ok, czy w takim razie dobrze rozumiem, że odcinki, półproste itd. możemy przedłużać w każdą stronę, ale po prostu przedłużenie w naszym przykładzie za punktem O, nie będzie należało do tej półprostej, a jedynie będzie jej przedłużeniem? Jeśli napisałam niezrozumiałe, proszę napisać, a spróbuję się poprawić

chichi: Rozumiem, tak dobrze myślisz. Tak samo jak możemy przedłużyć bok trójkąta etc.

Karolina: Dziękuję bardzo

Karolina: Zastanawiam się jeszcze nad ostatnią kwestią: ,,Jeśli podany jest kąt BOC w stosunku 1:3 to również wydaje mi się, że przy podawaniu stosunku kolejność powinna zostać zawsze zachowana, więc jedynie kąt BOX =α oraz kąt XOC = 3α, co z kolei powinno wykluczyć istnienie dwóch przypadków." W czym tutaj źle myślę? Z góry bardzo dziękuję.

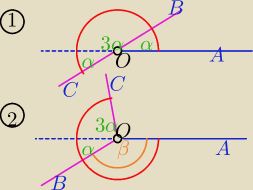
Eta: 1/ 5α=225^o ⇒ α=45^o α=45^o , 4α=180^o <AOB=45^o , <BOC=180^o ===================== 2/ 4α+β=225^o i α+β=180^o − −−−−−−−−−−−−− 3α=45^o ⇒ α=15^o <AOB=β=165^o , < BOC= 4α=60^o ===========================

Karolina: Dziękuję ❤️

Karolina: Jeśli chodzi o punkt 3) chodzi mi o to, że skoro w treści zadania jest napisane, że kąt BOC jest podzielony w stosunku 1:3, to dlaczego przyjmujemy również że jest on podzielony w stosunku 3:1, żeby istniał drugi przypadek? O stosunku 3:1 kąta BOC w treści zadania nie było nic napisane. Jeśli napisałam coś niezrozumiale, proszę napisać, postaram się poprawić Z góry bardzo dziękuję😊

Eta: |AC|: |CB|=1:3 ⇔ |CB| : |AC|=3:1

Karolina: A jak to się wiąże z kątem podanym w treści zadania? Rozumiem, że BOC w 1:3 oraz COB w 3:1 to to samo, ale to nadal nie jest to co na rysunku, czyli BOX=3α, OXC=α lub BOX=β oraz OXC=3β.

Karolina: Chyba że w kątach nie obowiązuje kolejność przy podawaniu stosunku? Chodzi mi o to, że np. dla stosunku 4:5 róż do tulipanów będzie tylko i wyłącznie: 4x: róże, 5x: tulipany, nie ma możliwości napisania na odwrót tzn. 5x: róże, 4x: tulipany, natomiast w kątach zostało to podane również na odwrót.

Eta: W bukiecie złożonym z róż i tulipanów stosunek ilości róż do ilości tulipanów jest równy 4:5 Bukiet składa się z 27 kwiatów ile jest w tym bukiecie róż a ile jest tulipanów ? Jaki jest stosunek ilości tulipanów do ilości róż ?

Karolina: Właśnie. Tulipanów do róż będzie 5:4, a róż do tulipanów 4:5. Dlaczego więc nie powinno być również napisane BOC w stosunku 1:3 lub BOC w stosunku 3:1 skoro oczekuje się od rozwiązującego rozpatrzenia dwóch przypadków?

Eta: bo właśnie ... sama masz rozważyć te przypadki 1:3 lub 3:1

Karolina: Czy to znaczy, że w kątach nie obowiązuje zasada kolejności podawania stosunku, skoro mogę ją sobie sama zmieniać?