Zadanie z twierdzenia cosinusów. Czy ktoś pomoże? Malwina: W trójkącie ABC długości środkowej BK i boku BC są równe 27, a długość boku AB jest równa 29. Oblicz pole trójkąta ABC.

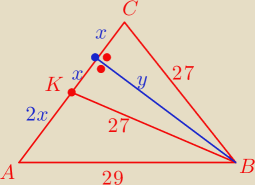
janek191: Mamy x² + y² = 27² = 729 (3 x)² + y² = 29² = 841 Odejmujemy stronami 8 x² = 112 x² = 14 x = √14 ======== y² = 729 − 14 = 715 y = √715 =========== Pole Δ P = 0,5*4x*y = 2 x*y = 2√14*√715 =2 √10 010

janek191: Tw. kosinusów 27² = 4x² + 27² − 4x*27*cos C 29² = 16x² + 27² − 8x*27*cos C 4 x² = 4x*27*cos C x = 27*cos C 112 = 16 x² − 8 x*27*cos C 112 = 16*27²*cos²C − 8*27*27*cos² C 112 = 16*27² cos² C − 8*27² cos²C 112 = 8*27² cos² C / : 8 14 = 27² cos² C

	14
cos2 C =
	272

	√14
cos C =
	27

więc x = √14 I AC I = 4 x = 4√14 itd.