Optymalizacja maturaek: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Do przyprostokątnej AC poprowadzono prostą równoległą przecinającą bok AB w punkcie D i bok BC w punkcie E. Długość odcinka DE wynosi 2, a CE wynosi 3. Niech x oznacza długość przyprostokątnej AC. Dla jakiej długości ich przeciwprostokątna ma najmniejszą długość? Jak wyznaczyć tu funkcję?

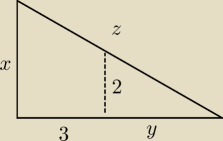
wredulus_pospolitus: z tw. Pitagorasa: z² = x² + y² z tw. Talesa:

y		y+3		2y+6
	=		−−−> x =
2		x		y

	2y+6		4y2 + 24y + 36
Z(x,y) = x2 + y2 = (		)2 + y2 =		+ y2 =
	y		y2

	24		36
= y2 + 4 +		+
	y		y2

Z'(y) = .... i szukasz minimum lokalnego (pamiętaj, że y > 0)