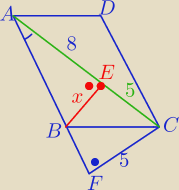
 I AF I =12 z tw. Pitagorasa
oraz
I AF I =12 z tw. Pitagorasa
oraz
| x | 5 | 10 | |||
= | ⇒ x = | ||||
| 8 | 12 | 3 |
 @ Janek
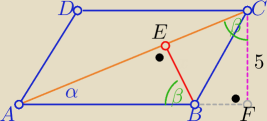
Pozwól , że poprawię ten Twój "dziwaczny" równoległobok
|AC|=13 z tw. Pitagorasa w ΔAFC : |AF|=√132−52= 12
z podobieństwa trójkątów AFC i ABE z cechy (kkk)
@ Janek
Pozwól , że poprawię ten Twój "dziwaczny" równoległobok
|AC|=13 z tw. Pitagorasa w ΔAFC : |AF|=√132−52= 12
z podobieństwa trójkątów AFC i ABE z cechy (kkk)
| x | 8 | 10 | |||
= | ⇒ x= | ||||
| 5 | 12 | 3 |