własności prawdopodobieństwa
mk: | | 1 | | 1 | | 1 | |
O zdarzeniach A,B e Omegi wiadomo, że P(A)= |
| , P(B)= |
| , P(AnB)= |
| . Oblicz |
| | 4 | | 3 | | 5 | |
P(A'nB').
Ja zrobiłam to tak, że jeżeli w jednym kole (omega) mamy dwa mniejsze A i B, to P(A'nB') będzie
cała zawartość koła − te dwa małe koła A i B (sory nie mam rysunku, ale mam nadzieję, że
wiadomo o co mi chodzi)
Czyli: P(A'nB')=1− (P(A)+P(B))+ P(AnB) (tutaj plus, bo P(AnB) policzyliśmy podwójnie przy
dodawaniu sumy P(A) i P(B))
Jedynka to jakby omega (w sensie jakby pełne prawdopodobieństwo, 100%)
Wyniki z tego wyszły mi dobrze, ale nie wiem czy pomysł jest poprawny. Może kompletnie się
mylę. Tak intuicyjnie do tego podeszłam.
Sprawdzi ktoś?
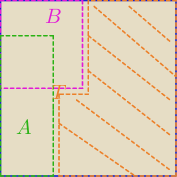 Dodam ilustrację do wpisu wredulusa:
P(A'nB')= 1 − P(AuB)
Dodam ilustrację do wpisu wredulusa:
P(A'nB')= 1 − P(AuB)