czworobok kw17: ABCD jest czworobokiem wypukłym. AC i BD przecinają się w E. Biorąc pod uwagę, że pola trójkąta ABE i trójkąta CDE wynoszą odpowiednio 4 i 9, znajdź najmniejszą możliwą wartość pola czworoboku ABCD.

Eta: P_min=25

wredulus_pospolitus:

	1
1) PΔ =		a*b*sinα gdzie α to kąt pomiędzy bokami a,b
	2

2) związku z tym, przy stałej długości boków a,b ... pole trójkąta będzie największe dla sinα = 1 −−−> α = 90^o 3) związku z tym, przekątne tego czworoboku muszą przecinać się pod kątem prostym i wiemy, że:

a*b
	= 4 −−−> a*b = 8
2

c*d
	= 9 −−−> c*d = 18
2

	a*c		b*d
pozostałe dwa trójkąty mają pola równe (w sumie)		+
	2		2

	4
F(a,c) = a*(9/c) + (4/a)*c = 9(a/c) +
	(a/c)

	4
F(x) = 9x +		−−−> minimum dla x = 2/3 i fmin = 12
	x

Stąd najmniejsze możliwe pole wynosi 12+4+9 = 25 [j²]

Eta:

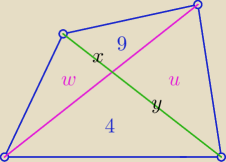
w		9		36
	=		⇒ wu=36 ⇒ w=
4		u		u

	36
P(u)=		+u+13
	u

P^'(u) = ............ ..................