Geometria, równoległobok Werve: Długości boków równoległoboku są równe 6cm i 10cm. Oblicz wysokości równoległoboku poprowadzone z wierzchołka kąta rozwartego wiedząc, że tworzą one kąt 60 stopni oraz wysokość DF znajduje się na przedłużeniu boku CB.

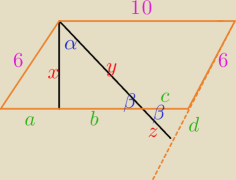
wredulus_pospolitus: 1) rysunek (dobry −−− u mnie to nie jest równoległobok, a jeśli nawet to proporcje nie są zachowane) 2) zaznacz trójkąty prostokątne, istotne będą 4 trójkąty −−− i odpowiednie długości 3) zaznaczamy kąt α = 60^o i na jego podstawie zaznaczamy kąt β = 30^o 4) wskazujemy, że: y = 2x ; b = √3x c = 2d ; z = √3d 3) tworzymy układ równań: x² + a² = 36 (2x+√3d)² + (d+6)² = 100 a+√3x +2d = 10 trochę mało przyjemnie to wygląda ... ale trzy równania, trzy niewiadome −−− można to wyznaczyć

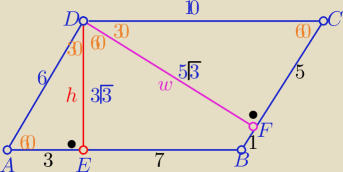
Eta: Z trójkątów "ekierek" o kątach ostrych 30^o, 606o h=3√3 i w =5√3 i po ptokach taka uwaga : Spodek F wysokości DF nie może leżeć na przedłużeniu BC bo wtedy |CF|=5 więc krótsze od BC

Eta: lub tak jeżeli h= 3√3 to w= 5√3 bo pole równoległoboku; P=3√3*10=30√3 = w*6 ⇒ w=5√3

wredulus_pospolitus: Etuś −−− a czemu zakładasz że ∡BAD = 60^o ? Na jakiej podstawie to czynisz ?

Eta: bo w ΔCFD |∡DCF|=60^o = |∡BAD|

Eta: bo w Δ CFD prostokątnym : |∡FDC|=30^o to |∡DCF|=60^o

Eta: Czy już jasne?

wredulus_pospolitus: jop ... pominąłem fakt, że tam (przy D) będzie kąt prosty po opuszczeniu wysokości na AB