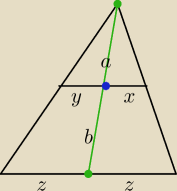
Geometria analityczna Werve: Wykaż ANALITYCZNIE, że środki podstaw, punkt przecięcia przekątnych i wierzchołek trójkąta powstały po przedłużeniu ramion trapezu ABCD są współliniowe.

wredulus_pospolitus: Wykażemy że środki podstaw trapezu i wierzchołek trójkąta powstały z przedłużenia ramion trapezu są współliniowe. 1) Rysunek 2) zaznaczamy środek dolnej podstawy i wierzchołek − prowadzimy prostą 3) mamy wykazać, że niebieska kropka jest środkiem górnej podstawy trapezu co czynimy poprzez zastosowanie tw. Talesa

a		a+b		a		a+b		a		a
	=		a także		=		−−−> stąd		=		−−−> y = x
y		z		x		z		y		x

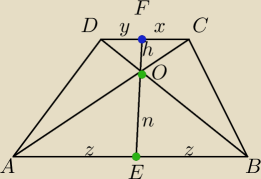wredulus_pospolitus: Wykażemy że środki ramion trapezu i przecięcie się przekątnych trapezu leżą na jednej prostej 1) Rysunek 2) zaznaczamy środek dolnej podstawy i punkt przecięcia się przekątnych − prowadzimy prostą 3) trójkąt AEO jest podobny do trójkąta CFO (podobieństwo kkk) 4) trójkąt BEO podobny do trójkąta DFO (podobieństwo kkk)

z

x

z

y

x

y

5) stąd

=

oraz

=

−−−>

=

−−−> x = y

n

h

n

h

h

h