Geometria dżemMorelowy: Punkty S₁ i S₂ są środkami okręgów stycznych zewnętrznie w ≤punkcie A. Przez punkt A poprowadzono prostą przecinającą okrąg o środku S₁ w punkcie K. a drugi z okręgów w punkcie L. Wykaż, że | kątAS1K|=|kątAS2L| .

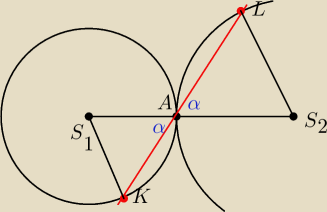
wredulus_pospolitus: krok 1: rysunek jak powyżej krok 2: zauważasz, że Δ_AKS1 jest równoramienny krok 3: zauważasz, że Δ_ALS2 jest równoramienny krok 4: powołując się na tw. o kątach wierzchołkowych (to chyba tak się nazywało) mamy kąt α tam gdzie mamy krok 5: idąc dalej tokiem rozumowania wykazujemy że kąty które mamy wykazać, że są równe, faktycznie są równe KOOOOONIEC